数组
数组
Table of Contents generated with DocToc (opens new window)
# 普通的数组相关题
# 1.(easy)移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
2
示例 2:
输入: nums = [0]
输出: [0]
2
思路1:
使用双指针,左指针指向当前已经处理好的序列的尾部,右指针指向待处理序列的头部。
右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移。
注意到以下性质:
左指针左边均为非零数;
右指针左边直到左指针处均为零。
因此每次交换,都是将左指针的零与右指针的非零数交换,且非零数的相对顺序并未改变。
代码:
class Solution {
public void moveZeroes(int[] nums) {
int left = 0;
int right = 0;
while (right < nums.length) {
if (nums[right] != 0) {
swap(nums, left, right);
left++;
}
right++;
}
}
public void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
思路2:
使用双指针,左指针始终指向0的位置,右指针指向非0位置。
- 如果当前左右指针都不为0,将两个指针都向后移一位
- 如果左指针为0,右指针不为0,交换,将两个指针都向后移一位
- 其他情况就只移动右指针即可
代码:
public void moveZeroes(int[] nums) {
int left = 0;
int right = 0;
while (right < nums.length) {
if (nums[left] != 0 && nums[right] != 0) {
left++;
}
else if(nums[left] == 0 && nums[right] != 0){
swap(nums,left,right);
left++;
}
right++;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# 2.(medium)和为K的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2 示例 2:
输入:nums = [1,2,3], k = 3 输出:2
思路1:
很容易想到利用前缀和,得出每个[0,i]区间的子数组之和,然后[i,j]区间之和就等于[0,j]-[0,i]。
求出前缀和以后,枚举所有区间前缀和之差,等于k就res加一。
时间复杂度为O(n2),空间复杂度O(1)
我的比官方暴力要快几百ms
代码:
class Solution {
public int subarraySum(int[] nums, int k) {
int res = 0;
int[] preSum = new int[nums.length];
preSum[0] = nums[0];
for(int i = 1;i<nums.length;i++){
preSum[i] = preSum[i-1]+nums[i];
}
for(int i = 0;i<preSum.length;i++){
if(preSum[i] == k){
res++;
}
for(int j = i+1;j<preSum.length;j++){
if(preSum[j]-preSum[i] == k){
res++;
}
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
思路2:
因为暴力的时间复杂度很高,我们可以利用hash表对算法进行优化。
暴力时我们使用的是 [0,j]-[0,i]==k 即是否存在两个前缀和之差等于k来寻找符合条件的[i,j]子数组。
我们可以换个思路,使用一个HashMap<Integer,Integer>(),将前缀和以key存入HashMap,value为这种前缀和出现的次数,
比如k=7,数组为:0 7 2 5 3 -1,前缀和为:0 7 9 14 17 16,
我们要找前缀和之间差为7的,只需要去map里面找每个前缀和,有多少个与它之差为7的。
所以我们把每个前缀和以及它的数量存入map,找到key为 当前前缀和-k,的前缀和的数量让res加上即可在O(1)内获得结果
这种思想的根本是,不是用区间(前缀和)去找差为K的区间数量,而是根据一个前缀和A,去找另一个满足A-B==K的前缀和B的数量
代码:
class Solution {
public int subarraySum(int[] nums, int k) {
int res = 0;
int pre = 0;
HashMap<Integer,Integer> map = new HashMap<>();
//先put一个0进去是为了nums[i]==k的情况,即只有一个元素的子数组
map.put(0,1);
for(int i=0;i<nums.length;i++){
pre+=nums[i];
if(map.containsKey(pre-k)){
res+=map.get(pre-k);
}
map.put(pre, map.getOrDefault(pre,0)+1);
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 3.(medium)在排序数组中查找元素的第一个和最后一个位置
class Solution {
public int[] searchRange(int[] nums, int target) {
int leftIdx = binarySearch(nums, target, true);
int rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return new int[]{leftIdx, rightIdx};
}
return new int[]{-1, -1};
}
public int binarySearch(int[] nums, int target, boolean lower) {
int left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 4.(medium)航班预订统计
这里有 n 个航班,它们分别从 1 到 n 进行编号。
有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座位。
请你返回一个长度为 n 的数组 answer,里面的元素是每个航班预定的座位总数。
示例 1:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5 输出:[10,55,45,25,25] 解释: 航班编号 1 2 3 4 5 预订记录 1 : 10 10 预订记录 2 : 20 20 预订记录 3 : 25 25 25 25 总座位数: 10 55 45 25 25 因此,answer = [10,55,45,25,25] 示例 2:
输入:bookings = [[1,2,10],[2,2,15]], n = 2 输出:[10,25] 解释: 航班编号 1 2 预订记录 1 : 10 10 预订记录 2 : 15 总座位数: 10 25 因此,answer = [10,25]
思路:
从题目例子不难看出,题目实际上就是给你一个长度为n,每个元素初始为0的int数组,让你对它进行多次[i,j,incr]操作,即对第i到第j个的值都加上incr(闭区间),很容易想到差分数组。
差分数组即differ[i] = nums[i]-nums[i-1],i>=1 (
differ[0]=nums[0]本身)所以对差分数组求前缀和,可以得到原数组
举例:
原数组: 1 2 3 4 5 6 9 原差分数组:1 1 1 1 1 3
对第3-5个加2:1 2 5 6 7 6 9 增加后: 1 3 1 1 -1 3
从例子可以看出,对原数组的[i,j]区间的数进行同时增加,相当于对差分数组differ:differ[i-1]+=incr,differ[j]-=incr
然后将差分数组differ求前缀和即可得到每个i位置
代码:
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int count = bookings.length;
int[] differ = new int[n];
for(int i=0;i<count;i++){
differ[bookings[i][0]-1] += bookings[i][2];
if(bookings[i][1]<n){
differ[bookings[i][1]] -= bookings[i][2];
}
}
for(int i=1;i<n;i++){
differ[i] += differ[i-1];
}
return differ;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
复杂度分析
- 时间复杂度:O(n+m),其中 n 为要求的数组长度,m 为预定记录的数量。我们需要对于每一条预定记录处理一次差分数组,并最后对差分数组求前缀和。
- 空间复杂度:O(1)。我们只需要常数的空间保存若干变量,注意返回值不计入空间复杂度。
# 5.(easy)爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶 示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
思路1:
因为只有两种爬楼梯方式,一次爬1个台阶或2个台阶,所以我们如果要爬到n个台阶,肯定是从第n-1个台阶或第n-2个台阶爬上去的,这样就可以得到爬到n的方式数量为 爬到n-1的方式数量+爬到n-2的方式数量,即f(n)=f(n-1)+f(n-2),是经典的斐波那契数列
代码:
class Solution {
//使用一个res中间变量
public int climbStairs(int n) {
int a = 1;
int b = 2;
int res = n;
for(int i=2;i<n;i++){
res = a+b;
a = b;
b = res;
}
return res;
}
//不使用中间变量
public int climbStairs(int n) {
if(n == 1 ||n == 2){
return n;
}
int a = 1,b = 2;
for(int i=2;i<n;i++){
b = a+b;
a = b-a;
}
return b;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 6.(medium)旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
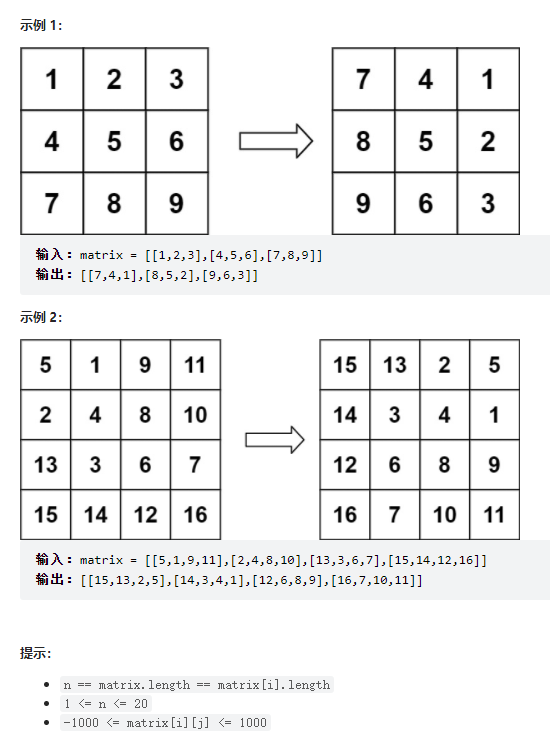
思路:
先将原数组按左上到右下的对角线交换元素,再将数组每一行反转即可得到数组顺时针旋转90度的图像
同理,先将原数组按右上到左下的对角线交换元素,再将数组每一行反转即可得到数组逆时针旋转90度的图像
代码:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//将数组按对角线反转
for(int i=0;i<n;i++){
for(int j=i;j<n;j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
//再反转每一行
for(int k=0;k<n;k++){
int i = 0,j = n-1;
while(i<j){
int temp = matrix[k][j];
matrix[k][j] = matrix[k][i];
matrix[k][i] = temp;
i++;
j--;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 7.(medium)螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
2
思路:
解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界:
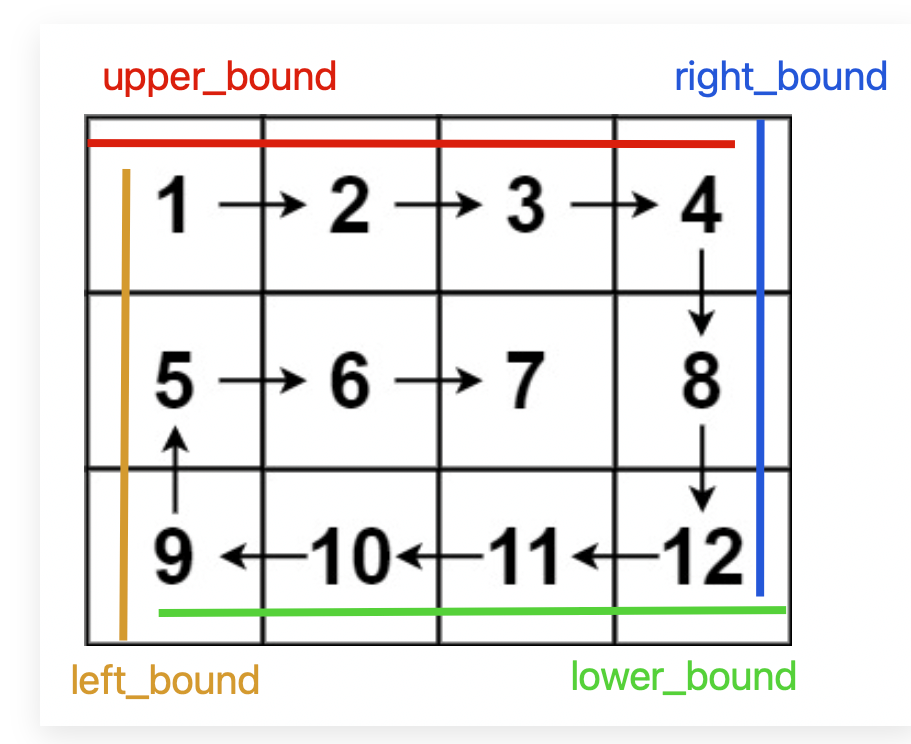
随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
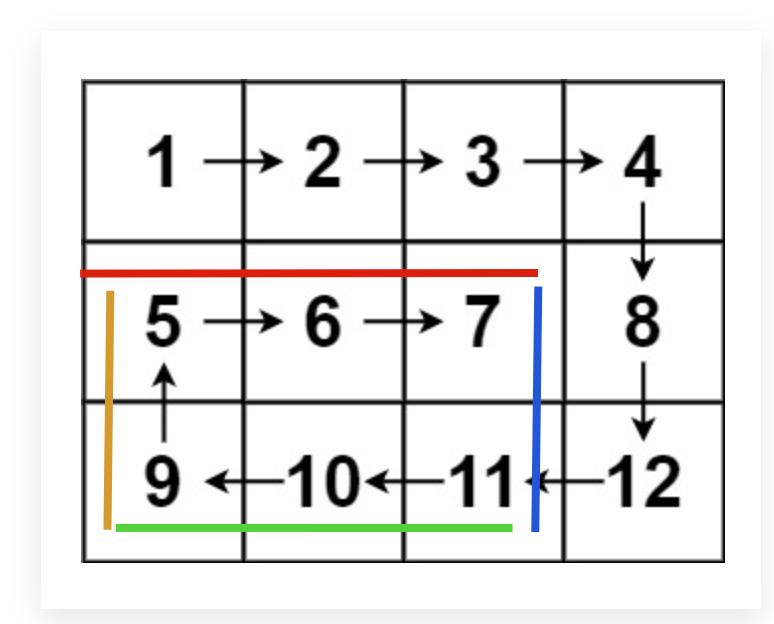
代码:
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int up = 0,down = m-1,left = 0,right = n-1;
List<Integer> res = new ArrayList<>();
while(res.size()<m*n){
if(up<=down){
//在顶部最左从左往右遍历
for(int k = left;k<=right;k++){
res.add(matrix[up][k]);
}
up++;
}
if(left<=right){
//在顶部最右从上往下遍历
for(int k = up;k<=down;k++){
res.add(matrix[k][right]);
}
right--;
}
if(up<=down){
//在底部最右从右往左遍历
for(int k = right;k>=left;k--){
res.add(matrix[down][k]);
}
down--;
}
if(left<=right){
//在底部最左从下往上遍历
for(int k = down;k>=up;k--){
res.add(matrix[k][left]);
}
left++;
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 8.(medium)螺旋矩阵||
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

思路与上题基本一致,只需要add到List的操作换成赋值为当前num即可
代码:
class Solution {
public int[][] generateMatrix(int n) {
int up = 0,down = n-1,left = 0,right = n-1;
int[][] res = new int[n][n];
int num = 1;
while(num<=n*n){
if(up<=down){
//在顶部最左从左往右遍历
for(int k = left;k<=right;k++){
res[up][k] = num++;
}
up++;
}
if(left<=right){
//在顶部最右从上往下遍历
for(int k = up;k<=down;k++){
res[k][right] = num++;
}
right--;
}
if(up<=down){
//在底部最右从右往左遍历
for(int k = right;k>=left;k--){
res[down][k] = num++;
}
down--;
}
if(left<=right){
//在底部最左从下往上遍历
for(int k = down;k>=up;k--){
res[k][left] = num++;
}
left++;
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 9.(easy)数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入: [2, 3, 1, 0, 2, 5, 3] 输出:2 或 3
限制:
2 <= n <= 100000
思路1:
哈希表,代码不赘述
思路2:
利用数字范围都在0~n-1,在没有重复数字的情况下,每个索引都对应着一个元素,在有重复数字的情况下,一个索引可以对应多个元素。
所以在循环时,我们
判断当前nums[i]与索引i是否相等,如果相等,不做操作,进入下一次循环,直到不等。不等的时候,先判断一下,将这个值nums[i]作为索引找到的值与nums[i]相不相等,如果找到的相等,证明这个nums[i]就是重复的元素了;如果不等,就将下标nums[i]和下标i的值交换:swap(nums,i,nums[i])。
代码:
class Solution {
public int findRepeatNumber(int[] nums) {
int i = 0;
while(i<nums.length){
//如果值和下标相等 跳过
if(nums[i] == i){
i++;
continue;
}
if(nums[nums[i]] == nums[i]){
return nums[i];
}
swap(nums,i,nums[i]);
}
return -1;
}
public void swap(int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 10.(easy)数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2
限制:1 <= 数组长度 <= 50000
思路:
众数的数量肯定比其他数要多,当现在没有众数的时候,我们可以设一个数为众数。
每次循环时,如果vote==0,证明此时没有众数,就让当前循环的num为众数,初始化它的个数vote为1,并进行下一次循环。
此时vote>0了,有众数,我们判断当前数是不是等于设定的众数,如果等于,则增加众数个数vote,否则减少个数,直到循环结束,res即为众数。
因为众数的数量总比其他数多,用其他数每次抵消一个众数,剩到最后的肯定是众数了。
代码:
class Solution {
public int majorityElement(int[] nums) {
int res = 0;
int vote = 0;
for(int num : nums){
if(vote == 0){
res = num;
vote++;
continue;
}
if(num == res){
vote++;
}else{
vote--;
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 11.(medium)构建乘积数组
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
思路:
使用两个数组分别维护第i个元素左边、右边的所有数的乘积。dp[i]表示第i个数之前或之后的所有数的乘积
对于左边:dp[i] = dp[i-1]*a[i-1],注意边界,i应该从1开始加
对于右边:dp[i] = dp[i+1]*a[i+1],注意边界,i应该从i-2开始减
所以两次循环记录左右dp数组,然后b[i] = left[i]*right[i]。
注:要注意判a为null或者空数组
代码:
class Solution {
public int[] constructArr(int[] a) {
if(a == null || a.length == 0){
return a;
}
int n = a.length;
int[] left = new int[n];
int[] right = new int[n];
int[] b = new int[n];
left[0] = right[n-1] = 1;
for(int i=1;i<n;i++){
left[i] = left[i-1]*a[i-1];
}
for(int i=n-2;i>=0;i--){
right[i] = right[i+1]*a[i+1];
}
for(int i=0;i<n;i++){
b[i] = left[i]*right[i];
}
return b;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 12.(medium)栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1] 输出:true 解释:我们可以按以下顺序执行: push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1 示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2] 输出:false 解释:1 不能在 2 之前弹出。
思路:
使用一个辅助栈模拟push/pop操作,循环入栈顺序数组,每次都将元素压入辅助栈,每次压入后判断,如果当前的辅助栈的栈顶元素就是出栈数组的下标位置的元素,那么将这个元素从辅助栈弹出,并移动出栈数组下标到后一位,循环结束后判断当前辅助栈是否为空即可,为空证明是可以实现的
代码:
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<Integer>();
int i = 0;
for(int pushNum : pushed){
stack.push(pushNum);
//当辅助栈栈顶是当前第一个要出栈的元素时 出栈 并切换要出栈的元素为下一个
while(!stack.isEmpty()&&stack.peek()==popped[i]){
stack.pop();
i++;
}
}
return stack.isEmpty();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 13.(easy)两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
思路:
暴力枚举复杂度O(n^2)就不说了。
优化方法:不是去找a+b=target,而是找有没有一个a,满足a=target-b或者一个b满足b=target-a,如果不返回下标,用HashSet存元素然后每次循环前先判断之前的元素有没有等于target-nums[i]的就行。题目要求返回下标,所以用HashMap存值和下标的映射即可,时间、时间复杂度均为O(N)
代码:
class Solution {
public int[] twoSum(int[] nums, int target) {
//用map找 target-nums[i]是否存在于map中
Map<Integer,Integer> map = new HashMap<>();
for(int i=0;i<nums.length;i++){
if(map.containsKey(target-nums[i])){
return new int[]{map.get(target-nums[i]),i};
}
map.put(nums[i],i);
}
return new int[]{-1,-1};
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# 二分查找、双指针相关
# 1.(easy)二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4 示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。 n 将在 [1, 10000]之间。 nums 的每个元素都将在 [-9999, 9999]之间。
思路:
有序数组,使用二分查找,以nums[mid]与target的大小关系决定应该往右边找还是往左边找
代码:
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]==target){
return mid;
}else if(nums[mid]>target){
right = mid-1;
}else if(nums[mid]<target){
left = mid+1;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 2.(easy)在排序数组中查找数字 1
统计一个数字在排序数组中出现的次数。
示例 1:
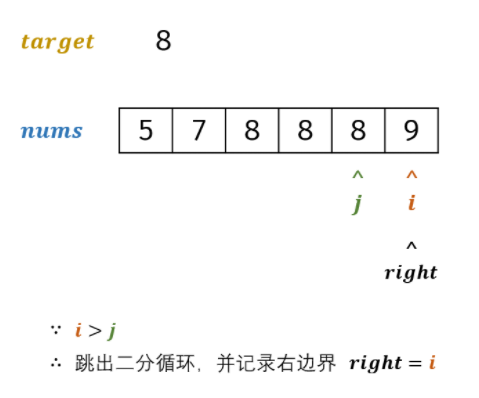
输入: nums = [5,7,7,8,8,10], target = 8 输出: 2 示例 2:
输入: nums = [5,7,7,8,8,10], target = 6 输出: 0
提示:
0 <= nums.length <= 105 -109 <= nums[i] <= 109 nums 是一个非递减数组 -109 <= target <= 109
思路:
常规是直接一趟循环记录target数量即可,时间复杂度为O(n),没有利用到数组是非递减 这个条件;
使用二分:
我们的目的是找到第一个大于target的元素位置和第一个小于target的元素位置
找第一个大于target的元素位置
我们寻找当前数组范围内的mid值,如果nums[mid]大于目标值,右指针对mid左移一位,如果
小于等于目标值,则左指针对mid右移一位。注意小于等于这个判断条件这里,小于的时候,右移是毋庸置疑的;等于的时候也要继续右移,就是要找下一个可能比mid大的,当左右指针到达同一位置时,mid也为这个位置,如果num[mid]大于目标值,那么右指针right左移一位,现在left>right了,循环结束,此时的left所在位置,即为边界位置,即第一个大于target的元素位置找第一个小于target的元素位置
与1相似,只是在判断如果nums[mid]
大于等于目标值的时候,都要左移,以便找到第一个小于target的元素位置
复杂度分析:
- 时间复杂度O(logN): 二分法为对数级别复杂度。
- 空间复杂度O(1): 几个变量使用常数大小的额外空间。
代码:
class Solution {
public int search(int[] nums, int target) {
int leftBound = 0;
int rightBound = 0;
int left = 0;
int right = nums.length-1;
//找右边界:即第一个大于target的元素位置
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]>target){
right = mid-1;
}else if(nums[mid]<=target){
left = mid+1;
}
}
//这里的left是右边界是因为mid在最后一次循环走到target位置
//然后在判断中 left = mid+1,mid是target位置,mid+1就是右边界
//此时的right就是最后一个元素的位置,left就是right+1,就是右边界
//已找到右边界 以右边界作为重新搜索的右边界
rightBound = left;
left = 0;
//找左边界 即第一个小于target的元素位置
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]>=target){
right = mid-1;
}else if(nums[mid]<target){
left = mid+1;
}
}
//这里的right是左边界是因为mid在最后一次循环走到target位置
//然后在判断中 right = mid-1,mid是target位置,mid-1就是左边界
//此时的left就是第一个元素的位置,right就是left-1,就是左边界
leftBound = right;
return rightBound-leftBound-1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 3.(medium)在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
进阶:
你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗?
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4] 示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1] 示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
思路:
与上一题类似,上一题是要找一个数子在
排序数组中出现的次数,即找到它第一次出现的位置和最后一次出现的位置即可。此题也一样,找到第一次出现位置和最后一次出现位置
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
int left = findLeft(nums,target);
int right = findRight(nums,target);
if (left <= right && nums[left] == target) {
return new int[]{left,right};
}
return new int[]{-1,-1};
}
//找左边的
public int findLeft(int[] nums,int target){
int left = 0;
int right = nums.length-1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]>=target){
right = mid-1;
}else{
left = mid+1;
}
}
//此时的right就是左边界 因为right比left小1
return left;
}
//找右边的
public int findRight(int[] nums,int target){
int left = 0;
int right = nums.length-1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]<=target){
left = mid+1;
}else{
right = mid-1;
}
}
//此时的left就是右边界 因为left比right大1
return right;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 4.(easy)排序数组中两个数字之和
给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 0 开始计数 ,所以答案数组应当满足 0 <= answer[0] < answer[1] < numbers.length 。
假设数组中存在且只存在一对符合条件的数字,同时一个数字不能使用两次。
思路:
因为数组是升序排列,所以可以使用左右指针,每次计算左右指针数之和,如果大于target,说明右边的数太大了,右指针减一,如果小于target,说明左边的数小了,左指针加一,直到和等于target就break,或左右指针相遇退出循环(因为题目保证会存在且只存在一对符合条件的数字,同时一个数字不能使用两次)
代码:
class Solution {
public int[] twoSum(int[] numbers, int target) {
int left = 0;
int right = numbers.length-1;
int sum = 0;
while(left<right){
sum = numbers[left]+numbers[right];
if(sum>target){
right--;
}else if(sum<target){
left++;
}else{
break;
}
}
return new int[]{left,right};
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 5.(medium)两数之和2
题目与上题类似,只是数组规定下标从1开始,返回的结果下标都加1即可,纯双指针解法不再赘述
更好的解法:二分+双指针
- 先二分判断如果left+mid大于target,那么可以直接更新right到mid-1;
- 二分判断如果right+left小于target,那么可以直接更新left到mid+1;
- 后面的操作和纯双指针一样
在最好的情况下,每次都走二分,时间复杂度为O(logN),最坏的情况为纯双指针,复杂度O(N)
代码:
class Solution {
public int[] twoSum(int[] numbers, int target) {
int left = 0;
int right = numbers.length-1;
int sum = 0;
while(left<right){
int mid = left+(right-left)/2;
sum = numbers[left]+numbers[right];
if(numbers[left]+numbers[mid]>target){
right = mid-1;
}else if(numbers[mid]+numbers[right]<target){
left = mid+1;
}else if(sum>target){
right--;
}else if(sum<target){
left++;
}else{
return new int[]{left+1,right+1};
}
}
return new int[]{left+1,right+1};
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 6.(easy)调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数在数组的前半部分,所有偶数在数组的后半部分。
示例:
输入:nums = [1,2,3,4] 输出:[1,3,2,4] 注:[3,1,2,4] 也是正确的答案之一。
提示:
0 <= nums.length <= 50000 0 <= nums[i] <= 10000
思路:
看到分成两部分,想到双指针,当左指针遇到偶数停下,右指针遇上奇数停下,然后交换,base case是当左右指针相遇
代码:
注:使用与1运算提高执行速度
class Solution {
public int[] exchange(int[] nums) {
int left = 0,right = nums.length-1;
while(left<right){
while(left<right&&(nums[left]&1)!=0){
left++;
}
while(left<right&&(nums[right]&1)==0){
right--;
}
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
}
return nums;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 7.(easy)0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
输入: [0,1,3]
输出: 2
2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
2
思路1:
题目要求的就是数组下标值i不等于nums[i]时的i,可以想到使用循环遍历
代码:
class Solution {
public int missingNumber(int[] nums) {
int i;
for(i = 0;i<nums.length;i++){
if (i != nums[i]) {
return i;
}
}
return i;
}
}
2
3
4
5
6
7
8
9
10
11
思路2 二分:
因为数组是增序排序数组,一般看到这个特性,又是在数组中查找元素,基本都可以使用二分。
二分要找的是,第一个nums[i]大于i的元素。
进行二分的时候
当i<=j时循环(当闭区间[i,j]为空时跳出)
如果mid所在位置的元素nums[mid]==mid,证明要找的位置肯定在mid后面,即(mid,j]
如果mid所在位置的元素nums[mid]!=mid,证明要找的位置肯定在mid前面,即[i,mid)
跳出时,变量i和j分别指向
第一个nums[i]大于i的元素和最后一个nums[i]等于i的元素。因此返回i即可。如:[0,1,2,3,4,5,6,7,9] 8
i,j的指向是上面的原因是,i,j走到同一位置7,然后此时的mid就是7,此时的7是等于nums[7]的,所以i会+1,走到8,此时的8!=num[8]->9,所以此时的i就是我们要求的下标
代码:
class Solution {
public int missingNumber(int[] nums) {
int i = 0,j = nums.length-1;
while(i<=j){
int mid = i+(j-i)/2;
if(mid == nums[mid]){
//如果等于 那么肯定在(mid,j]
i = mid+1;
}else {
//如果不等 肯定在[i,mid)
j = mid-1;
}
}
return i;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 8.(easy)旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。
请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], ..., a[n-1]]旋转一次的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
示例 1:
输入:numbers = [3,4,5,1,2] 输出:1 示例 2:
输入:numbers = [2,2,2,0,1] 输出:0
思路:
以[3,4,5,1,2,2]为例:初始numbers[left]=0,numbers[right]=2; left=0,right=5;
- 当mid为2时,numbers[mid]=5,此时它比numbers[right]=2要大,证明旋转的点肯定在5的前面,所以left=mid+1缩小区间
- 下一次,left=3,right=5,mid=4,此时numbers[mid]=2,与numbers[right]相等,这种情况我们之间减小right缩小区间即可
- 下一次,left=3不变,right=4,mid=3,此时numbers[mid]=1,它小于numbers[right],证明旋转点在区间[left,mid]中,所以我们缩小right,right=mid;此时right=3
- 到这一步,left和right都等于3了,循环结束,证明已经找到,返回numbers[left]即可
代码:
class Solution {
public int minArray(int[] numbers) {
int length = numbers.length;
int left = 0,right = length-1;
while(left<right){
int mid = left+(right-left)/2;
//这种情况 最小值肯定在(mid,right]
if(numbers[mid]>numbers[right]){
left = mid+1;
}
//如果当前mid值小于右边的值 最小值肯定在[left,mid]
else if(numbers[mid]<numbers[right]){
right = mid;
}
//如果相等 无法判断m在哪个排序数组中,即无法判断旋转点x在[i,m]还是[m+1,j]区间中
//直接减小right缩小区间即可
else {
right--;
}
}
return numbers[left];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 9.(medium)三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = [] 输出:[] 示例 3:
输入:nums = [0] 输出:[]
思路:
一开始想和找两数之和一样,回溯写,但是有特例要超时,因为回溯的时间复杂度是O(n^3),所以使用双指针优化到O(n^2)就可以通过。
现将数组排序,用三个指针,k指针从0开始,直到nums.length-2,然后left每次从k+1开始,right每次为nums.length-1,我们要循环找,以nums[k]为基点,满足nums[k]+nums[left]+nums[right]==0的三个数。
而因为是排好序的,如果nums[k]大于0了,那么后面的nums[k]+nums[left]+nums[right]肯定也大于0,所以当前k及其后面的都不用考虑,直接break。
因为不允许有重复的三元组,所以当nums[k]与nums[k-1]重复的时候,需要continue;
和小于0的时候,增大left指针(如果nums[left]==nums[left+1]还要继续增加,所以用一个while(left<right && nums[left] == nums[++left]),这样就可以保证不会有重复的三元组,同理和大于0的时候也一样,右指针减小即可。
当和满足等于0时,将数加入res,left、right同时移动即可
代码:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
if(nums.length < 3){
return res;
}
Arrays.sort(nums);
//找满足num[k]+nums[left]+nums[right]=0的
//left每次初始化在k+1的位置 right初始化在nums.length-1
//nums.length-2保证后面还有两个数
for(int k=0;k<nums.length-2;k++){
//k大于0了 后面的left+right+k肯定也大于0 不用继续找了
if(nums[k] > 0){
break;
}
//如果这个k和前一个相等 跳过 因为找的是重复的组合
if(k>0&&nums[k]==nums[k-1]){
continue;
}
int left = k+1,right = nums.length-1;
while(left<right){
int sum = nums[k]+nums[left]+nums[right];
if(sum==0){
res.add(Arrays.asList(nums[k],nums[left],nums[right]));
while(left<right && nums[left] == nums[++left]);
while(left<right && nums[right] == nums[--right]);
}else if(sum>0){
while(left<right && nums[right] == nums[--right]);
}else{
while(left<right && nums[left] == nums[++left]);
}
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 10.(medium)搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
思路:
排序数组,又要时间复杂度O(logN),想到二分,如何二分?
将数组一分为二,其中一定有一个是有序的,另一个可能是有序,也能是部分有序。 此时有序部分用二分法查找。无序部分再一分为二,其中一个一定有序,另一个可能有序,可能无序。就这样循环我们通过nums[mid]与左值nums[left]进行比较:
- 当nums[mid]>=nums[left]的时候,证明[left,mid]这段是
有序递增的,此时就可以讨论情况:
- 如果target<nums[mid]且target>=nums[left],即target在左半区间[left,mid-1]
- 否则在右半区间[mid+1,right]
- 当nums[mid]<nums[left]的时候,证明[left,mid]这一段是包含旋转点的一段,也分两种情况讨论:
- 如果target>nums[mid]且target<=nums[right],证明[mid,right]这一段是
有序递增的,且target就在这个右半区间- 否则在左半区间
# 11.(medium)下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。 类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。 给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间
思路:
这道题说得复杂,其实本质是将整个数组的数字连起来看成一个数值,要我们找到一个
由这些数字组成的、大于原数值的最小的一个数
- 先倒序遍历数组,找到第一对左边数小于右边数的组合(nums[i-1]<nums[i]),然后记录下来,如果没有的话,证明整个数组是降序的,只需要升序排序整个数组然后return即可
- 找到上述组合后不能直接将两者交换,因为并不一定就是满足条件的。小的数为nums[i-1],需要继续从[i,nums.length-1]这段区间里面,找到
大于这个nums[i-1]的最小值,如果找得到,就将两者交换,然后将nums[i-1]后面的升序排一下来保证最小;如果找不到,证明[i,nums.length-1]区间是降序的,只需将其升序排一下即可
代码:
class Solution {
public void nextPermutation(int[] nums) {
int minIndex = -1;
//从后往前找第一对 前一个数(左)小于后一个数(右)的位置
for(int i=nums.length-1;i>0;i--){
if(nums[i]>nums[i-1]){
//找到小的那个位置
minIndex = i-1;
break;
}
}
//如果没有 证明数组是降序的 没有下一个排列 排序整个数组返回
if(minIndex == -1){
Arrays.sort(nums);
return;
}
//在区间(minIndex,nums.length-1]找大于nums[minIndex]的最小值
int largeIndex = -1;
for(int i=minIndex+1;i<nums.length;i++){
//如果这个小值后面有比它大的 找到大值中最小的与它交换
if(nums[minIndex] < nums[i]){
//如果此时的这个大于小值的数没被初始化 就初始化
if(largeIndex == -1){
largeIndex = i;
}
//否则取这个小值与nums[i]中的更小的
else{
if(nums[i]<nums[largeIndex]){
largeIndex = i;
}
}
}
}
/**
如果有 交换这个数与大于它的最小的数,没有就不交换 直接升序后面的数在返回即可
对这个数后面的进行升序的原因是 交换以后可能后面的部分还不是最小,所以需要升序一下来保证后面的部分最小
*/
if(largeIndex != -1){
swap(nums,minIndex,largeIndex);
}
//然后把这个数后面的升序排序 返回
Arrays.sort(nums,minIndex+1,nums.length);
}
public void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# 12.(medium)盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
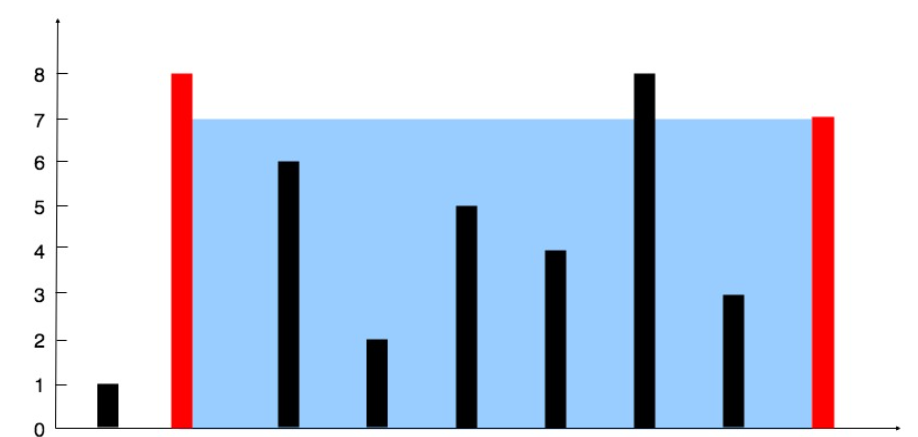
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。 示例 2:
输入:height = [1,1] 输出:1
思路:
我们用left、right两变量表示这个容器的两端的位置的下标,由题意可以得出,容器的容量等于
短的垂线*(right-left)(下标之差),即:s = Math.min(height[left],height[right])*(right-left);
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽底边宽度-1,所以影响水槽的容量的只有移动后某一条板是变长还是变短
- 若向内移动短板,水槽的短板min(height[left],height[right])可能会变大,因此下一个水槽的面积可能会增大
- 若向内移动长板,移动后的板如果仍然比现在的短板大,那么水槽的容量是不变的;如果移动后的板比现在的短板小,那么面积等于移动后的更小的板的长度*宽度,结果可能变小或者不变,所以移动长板的时候,水槽的短板min(height[left],height[right])可能不变或者变小,因此下一个水槽的面积会变小或者不变,所以我们每次只将短板进行移动向内移动,水槽容量才有可能会变大,所以一直移动短板即可
因此,初始化双指针分列水槽的左右两端,循环每轮将短板向内移动一格,并更新最大面积,直到两指针相遇时跳出,即可获得最大面积
代码:
class Solution {
public int maxArea(int[] height) {
int left = 0,right = height.length-1;
//条件是left<right 因为如果相遇就表示筛选完了
int max = Integer.MIN_VALUE;
while(left < right){
int result = compute(height,left,right);
max = Math.max(max,result);
if(height[left]>height[right]){
right--;
}else{
left++;
}
}
return max;
}
public int compute(int[] height,int left,int right){
return (right-left) * Math.min(height[left],height[right]);
}
}
//更简洁的写法
class Solution {
public int maxArea(int[] height) {
int i = 0, j = height.length - 1, res = 0;
while(i < j) {
res = height[i] < height[j] ?
Math.max(res, (j - i) * height[i++]):
Math.max(res, (j - i) * height[j--]);
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34