二叉树

Table of Contents generated with DocToc (opens new window)

递归
- 二叉树遍历框架
- 其他数据结构的遍历
重点
一、普通二叉树
二、二叉搜索树BST
三、二叉树递归转迭代
- 迭代遍历二叉树的代码框架
四、根据遍历结果还原二叉树
- 1.(medium)重建二叉树

# 递归

写递归算法的关键是要明确函数的定义是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要跳入递归的细节

# 二叉树遍历框架

void traverse(TreeNode root){
    if(root == null){
        return;
    }
    //前序遍历相关代码位置
    traverse(root.left);
    //中序遍历相关代码位置
    traverse(root.right);
    //后序遍历相关代码位置
}

1
2
3
4
5
6
7
8
9
10

# 其他数据结构的遍历

/* 迭代遍历数组 */
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {

    }
}

/* 递归遍历数组 */
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}

/* 迭代遍历单链表 */
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {

    }
}

/* 递归遍历单链表 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

单链表和数组的遍历可以是迭代的，也可以是递归的，二叉树这种结构无非就是二叉链表，不过没办法简单改写成迭代形式，所以一般说二叉树的遍历框架都是指递归的形式

# 重点

根结点是最顶上那个结点,金字塔的塔顶,叶子结点是最下面的结点,即没有子结点的结点

前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：

前序遍历位置的代码，会在刚遍历到当前节点 root，遍历 root 的左右子树之前执行；

中序遍历位置的代码，会在在遍历完当前节点 root 的左子树，即将开始遍历 root 的右子树的时候执行；

后序遍历位置的代码，会在遍历完以当前节点 root 为根的整棵子树之后执行。

# 一、普通二叉树

# 1.(`easy`)二叉树的前序遍历

class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }
    public void traverse(TreeNode root){
        if (root == null){
            return;
        }
        res.add(root.val);
        traverse(root.left);
        traverse(root.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

res.add(root.val);即在刚进入二叉树结点时执行

# 2.(`easy`)二叉树的深度

class Solution {
    int res = 0;
    int curDepth = 0;
    public int maxDepth(TreeNode root) {
        traverse(root);
        return res;
    }
    public void traverse(TreeNode root){
        if (root == null){
            res = Math.max(res, curDepth);
            return;
        }
        curDepth++;
        traverse(root.left);
        traverse(root.right);
        curDepth--;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

利用curDepth维护当前所在位置的深度，每到达一个结点curDepth++，离开该结点时，curDepth--，到达叶子结点后，更新一下最大深度

另一种解法：

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftMaxDepth = maxDepth(root.left);
        int rightMaxDepth = maxDepth(root.right);
        //返回左右子树深度大的  +1是加上根节点
        return Math.max(leftMaxDepth,rightMaxDepth)+1;
    }
}

1
2
3
4
5
6
7
8
9
10
11

# 3.(`easy`)翻转二叉树

核心思路是将每个结点的左右子结点交换即可，可以在前序位置或后续位置进行交换，最后返回root即可

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return null;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 4.(`medium`)二叉树的层序遍历

迭代方式

利用队列按从左到右的顺序储存每一层的所有结点，每次for循环将这些结点组合成List< Integer>,添加到res列表中，注意的是，for循环的次数，是当前这次while循环中队列的size()，而不是直接队列的size()；

每次while循环用于控制层数

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Deque<TreeNode> nodeDeque = new LinkedList<>();
        nodeDeque.push(root);
        while (!nodeDeque.isEmpty()){
            //对当前队列中的每个结点进行处理
            List<Integer> temp = new ArrayList<>();
            //当前层的结点数量
            int curLen = nodeDeque.size();
            for (int i = 0; i < curLen; i++) {
                TreeNode curNode = nodeDeque.pop();
                temp.add(curNode.val);
                //把当前结点的左右子结点都入队列
                if (curNode.left != null){
                    nodeDeque.add(curNode.left);
                }
                if (curNode.right != null){
                    nodeDeque.add(curNode.right);
                }
            }
            res.add(temp);
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 5.(`medium`)N叉树的层序遍历

迭代方式

同二叉树的层序遍历类似，只是结点的结构换成了

class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

只需改变入队列时的对象为当前结点的每个子结点即可

代码：

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Deque<Node> nodeDeque = new LinkedList<>();
        nodeDeque.push(root);
        while (!nodeDeque.isEmpty()){
            //对当前队列中的每个结点进行处理
            List<Integer> temp = new ArrayList<>();
            int curLen = nodeDeque.size();
            for (int i = 0; i < curLen; i++) {
                Node curNode = nodeDeque.pop();
                temp.add(curNode.val);
                List<Node> children = curNode.children;
                for (int j = 0; j < children.size(); j++) {
                    //把当前结点的所有子结点都入队列
                    nodeDeque.add(children.get(j));
                }
            }
            res.add(temp);
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 6.(`medium`)填充每个结点的下一个右侧结点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

1
2
3
4
5
6

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

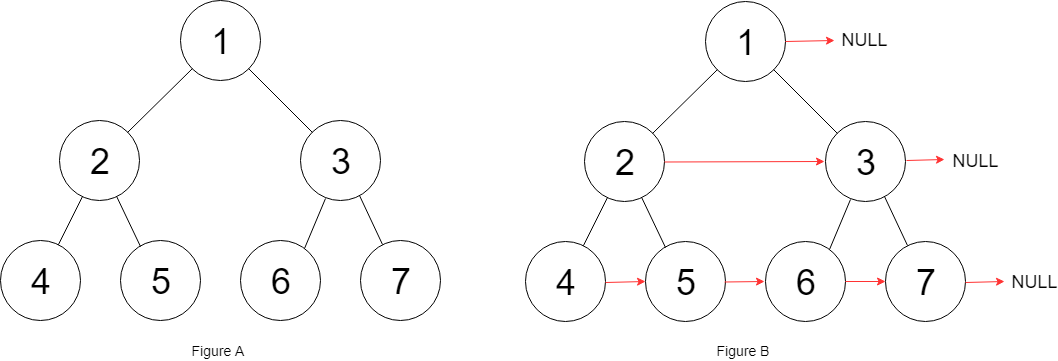
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

1
2
3

示例 2:

输入：root = []
输出：[]

1
2

提示：

树中节点的数量在 [0, 212 - 1] 范围内
-1000 <= node.val <= 1000

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

解题思路：

利用层序遍历

利用二叉树层序遍历的思想，将每层的每两个左右结点之间由左连到右

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if (root == null){
            return root;
        }
        Node res = root;
        LinkedList<Node> nodeDeque = new LinkedList<>();
        nodeDeque.push(root);
        while (!nodeDeque.isEmpty()){
            //对当前队列中的每个结点进行处理
            Node left = nodeDeque.get(0);
            for (int i = 1; i < nodeDeque.size(); i++){
                //每个左边的结点都和它右边的连上 不管是在同一结点上还是跨结点
                left.next = nodeDeque.get(i);
                //连上以后 将右边的结点作为左结点 继续连
                left = nodeDeque.get(i);
            }
            int curLen = nodeDeque.size();
            for (int i = 0; i < curLen; i++) {
                Node curNode = nodeDeque.pop();
                //把当前结点的左右子结点都入队列
                if (curNode.left != null){
                    nodeDeque.add(curNode.left);
                }
                if (curNode.right != null){
                    nodeDeque.add(curNode.right);
                }
            }
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

使用递归

先将在同一父节点下的两个结点连接好，然后连接不同父节点的结点。

因为连接不同父节点的结点时，同一父节点下的两个结点已经被连接好了，而根据题目定义，我们只需要将已个有子节点的结点的右子节点与另一个有子节点的结点的左结点连接起来就行了

class Solution {
    public Node connect(Node root) {
        if (root == null){
            return root;
        }
        connectTwo(root.left,root.right);
        return root;
    }
    public void connectTwo(Node node1,Node node2){
        if (node1 == null || node2 == null) {
            return;
        }
        node1.next = node2;
        connectTwo(node1.left,node1.right);
        connectTwo(node2.left, node2.right);
        connectTwo(node1.right, node2.left);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 7.(`easy`)二叉树的直径

我们知道，二叉树的直径为左右子树最大深度之和，问题转化为求子树最大深度，然后取直径与深度之和的max即可。

使用后序遍历，定义int maxDepth方法返回每个结点的最大深度，在方法中的后序遍历代码位置，取直径与深度之和的max

class Solution {
    int diameter = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return diameter;
    }

    public int maxDepth(TreeNode root){
        if (root == null){
            return 0;
        }
        int leftMaxDepth = maxDepth(root.left);
        int rightMaxDepth = maxDepth(root.right);
        //计算直径
        diameter = Math.max(diameter,leftMaxDepth+rightMaxDepth);

        //返回深度 加1是加上根节点自己
        return 1+Math.max(leftMaxDepth, rightMaxDepth);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 8.(`easy`)对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

使用层序遍历，比较每一层是否轴对称

使用层序遍历比较每一层是我们容易想到的方法，但要注意的是，题目要求的是中心对称，在使用中序遍历的时候

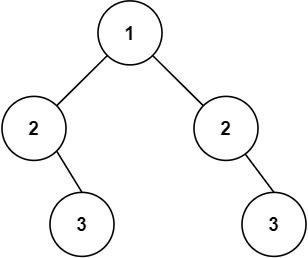
这种情况，中序遍历得到的结果是23132，进行判断的话是满足对称的，所以我们将缺一个子节点的二叉树补全成完全的二叉树，得到的结果：101 2 3 1 101 2 3，就可以区分这种情况了

代码:

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Deque<TreeNode> nodeDeque = new LinkedList<>();
        nodeDeque.push(root.left);
        nodeDeque.push(root.right);
        int count = 0;
        while (!nodeDeque.isEmpty()){
            //对当前队列中的每个结点进行处理
            Deque<Integer> res = new LinkedList<>();
            int curLen = nodeDeque.size();
            for (int i = 0; i < curLen; i++) {
                TreeNode curNode = nodeDeque.pop();
                //如果当前结点为空 就会加入101
                if (curNode == null){
                    res.add(101);
                    continue;
                }else{
                    res.add(curNode.val);
                    //结点放进去
                    nodeDeque.add(curNode.left);
                    nodeDeque.add(curNode.right);
                }
            }
            while (!res.isEmpty()){
                Integer first = res.pollFirst();
                Integer last = res.pollLast();
                if (first==null || last==null){
                    return false;
                }
                if (first != last){
                    return false;
                }
            }
        }
        return true;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

使用递归：

递归函数的定义是：判断以两个结点为根节点的子树是否对称，在函数中，需要判断这两个根节点是否相同，然后判断他们的左右子结点是否对称相同

代码：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        //不要忘了根节点为空的情况
        if (root == null){
            return true;
        }
        return judge(root.left, root.right);
    }

    public boolean judge(TreeNode left,TreeNode right){
        //没有子节点的情况 也是对称
        if (left == null&& right == null){
            return true;
        }
        if (left == null || right == null){
            return false;
        }
        if (left.val != right.val){
            return  false;
        }
        boolean judge = judge(left.left, right.right);
        boolean judge1 = judge(left.right, right.left);
        return judge&&judge1;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 9.(`easy`) 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

题目本质上就是只需要遍历两棵树的每一个结点，然后对每一个结点执行要求的合并操作即可，合并有两种思路

构造新的二叉树：

先合并root1和root2根节点，然后返回新的根节点，再递归合并root1、root2的左右子节点，然后赋给新的根节点的left和right

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null && root2 == null){
            return null;
        }
        TreeNode root = new TreeNode((root1==null?0:root1.val)+(root2==null?0:root2.val));
        root.left = mergeTrees(root1==null?null:root1.left, root2==null?null:root2.left);
        root.right = mergeTrees(root1==null?null:root1.right, root2==null?null:root2.right);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11

在原root1或root2上直接修改

不构造新的二叉树，而是使用root1(或root2)作为要返回的二叉树，直接在root1上进行修改即可。当root1和root2有一个为null时，直接返回另一个,即：如果一棵树有，另一棵树没有，接上去

class Solution {
 	public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null){
            return root2;
        }
        if (root2 == null){
            return root1;
        }
        root1.val = (root1==null?0:root1.val)+(root2==null?0:root2.val);
        root1.left = mergeTrees(root1==null?null:root1.left, root2==null?null:root2.left);
        root1.right = mergeTrees(root1==null?null:root1.right, root2==null?null:root2.right);
        return root1;
    }   
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 10.(`medium`)二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。展开后的单链表应该与二叉树先序遍历顺序相同。

示例 1：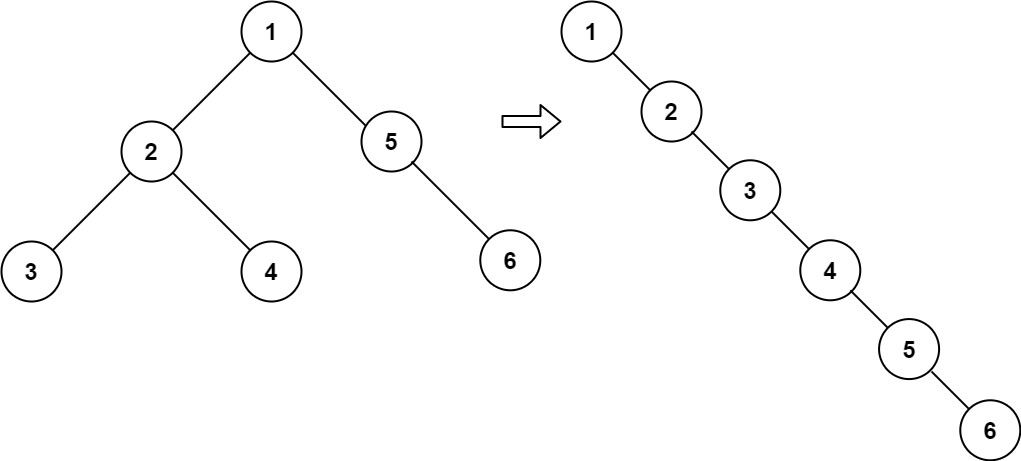

思路1：递归实现

flatten方法的定义是将以输入的节点为根的二叉树拉成一条链表，具体操作是：将根节点的right=左子节点，根节点的left=null，然后将原先的右子树接到当前又子树的末端

代码：

class Solution {
    /**
    方法的定义是将每个节点的右子节点接到左子节点的右子节点上
    然后将根节点的right=左子节点，根节点的left=null
     */
    public void flatten(TreeNode root) {
        if(root == null){
            return;
        }
        TreeNode left = root.left;
        TreeNode right = root.right;
        root.right = left;
        root.left = null;
        //将原先的右子树接到当前右子树的末端
        TreeNode p = root;
        while (p.right != null) {
            p = p.right;
        }
        p.right = right;
        flatten(root.left);
        flatten(root.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

思路2：迭代

将结点按先序遍历出来存到List里面，然后一个循环修改每个结点的指向即可

class Solution {
    List<TreeNode> res = new ArrayList<>();
    public void flatten(TreeNode root) {
        slove(root);
        for(int i = 0;i<res.size()-1;i++){
            res.get(i).right = res.get(i+1);
            res.get(i).left = null;
        }
    }
    public void slove(TreeNode root){
        if(root == null){
            return;
        }
        res.add(root);
        slove(root.left);
        slove(root.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

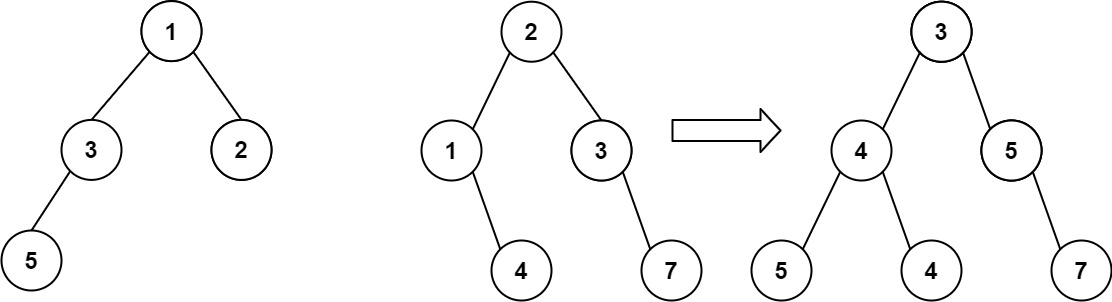
# 11.(`medium`)最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

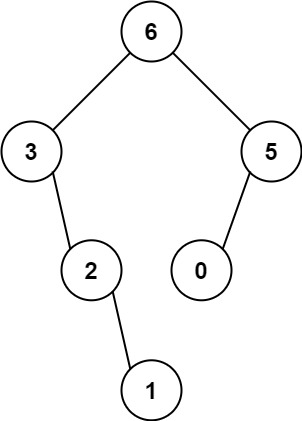
输入：nums = [3,2,1,6,0,5] 输出：[6,3,5,null,2,0,null,null,1] 解释：递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
[3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
空数组，无子节点。

[2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
空数组，无子节点。

只有一个元素，所以子节点是一个值为 1 的节点。

[0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
只有一个元素，所以子节点是一个值为 0 的节点。

空数组，无子节点。

思路：

创建一个根节点，其值为 nums 中的最大值。

递归地在最大值左边的 子数组前缀上 构建左子树。

递归地在最大值右边的 子数组后缀上 构建右子树。

如上所说的，例如nums[] = [3,2,1,6,0,5]，先找到6(下标为3)为作为根节点，然后在下标为[0-3)的数里面找最大的(下标为0)，作为左子结点，在下标为[4,5]的数里再找最大的(下标为5)，作为右节点，然后递归[4,5)，最大为0，即左子树为0，然后继续递归(0)，因为右边数组的前一个最大值的下标是0，即该位置左边已经没有数了，直接返回null即可，所以右子树为null

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums,0,nums.length);
    }

    public TreeNode construct(int[] nums,int start,int end){
        if (start >= end) {
            return null;
        }
        int max = -1;
        int index = -1;
        for (int i = start; i < end; i++) {
            if (nums[i] > max){
                max = nums[i];
                index = i;
            }
        }
        TreeNode rootNode = new TreeNode(max);
        rootNode.left = construct(nums,start,index);
        rootNode.right = construct(nums,index+1,end);
        return rootNode;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 12.(`medium`)寻找重复的子树

给定一棵二叉树 root，返回所有重复的子树。

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

示例 1：

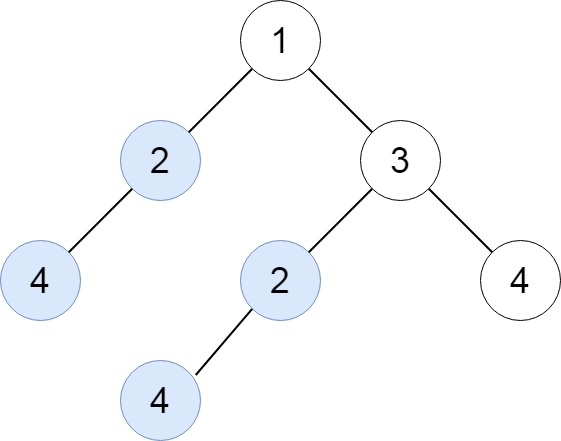
输入：root = [1,2,3,4,null,2,4,null,null,4]
输出：[[2,4],[4]]

1
2

思路：

我们可以将每个结点的，以它自己为根节点的子树，将子树的值序列化为字符串，以Map<Stirng,Integer>储存这种结构的子树出现的次数，在出现第二次的时候，将这个子树的根节点加入到结果List< TreeNode>即可。

具体的序列化方式就是，roo.val+","+left+","+right；这里的","可以换成任意的其它符号，left和right是递归返回的，以左右子节点为根的子树的序列化结果

代码：

class Solution {
    /**
     储存以每个结点为根结点的子树结构
     */
    List<TreeNode> res = new ArrayList<>();
    Map<String,Integer> map = new HashMap<>();
    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        find(root);
        Collections.reverse(res);
        return res;
    }
    public String find(TreeNode root){
        if(root == null){
            return "";
        }
        String left = find(root.left);
        String right = find(root.right);
        String tree = root.val+","+left+","+right;
        /*下面的部分可以换成这样
        map.put(tree,map.getOrDefault(tree,0)+1);
        Integer count = map.get(tree);
        if (count==2){
            res.add(root);
        }
        换了以后执行时间会低到只超过27%
        不换超过91%
        */
        Integer count = map.get(tree);
        if (count == null){
            map.put(tree,1);
        }else {
            map.put(tree,++count);
            if (count==2){
                res.add(root);
            }
        }
        return tree;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 13.(`easy`)二叉树的镜像

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

/
2 7 / \ /
1 3 6 9 镜像输出：

/
7 2 / \ /
9 6 3 1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

1
2

思路：

递归把以每个节点为根节点的子树的左右孩子交换即可。 root.left = right; root.right = left;

代码：

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        return mirror(root);
    }
    public TreeNode mirror(TreeNode root){
        if(root == null){
            return null;
        }
        TreeNode left = mirror(root.left);
        TreeNode right = mirror(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

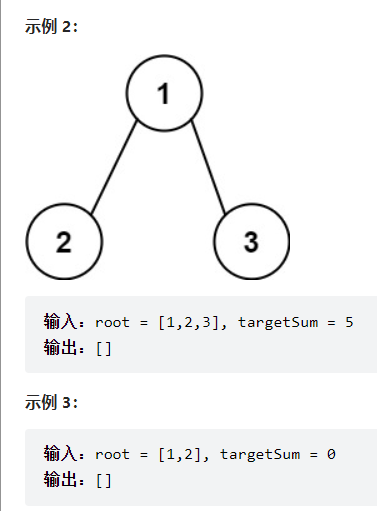
# 14.(`easy`)路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

示例 1：

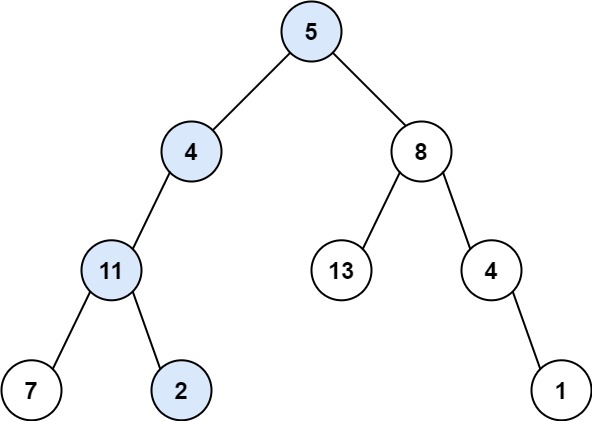
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

1
2
3

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

1
2
3

思路：

使用一个flag来标记是否存在target。在先序遍历位置，让target-当前节点的值，减完判断下，target是否为0，这里要注意，题目的要求是，到达叶子节点的路径综合为target，而叶子结点是指没有子节点的节点，所以判断时应该这样写
if(targetSum == 0 && root.left == null && root.right == null){
     flag = true;
}
1
2
3
然后每次后续遍历位置，即离开当前节点时，因为是要回到上一节点，应该将target的值加上当前节点值。

代码：

class Solution {
    boolean flag = false;
    public boolean hasPathSum(TreeNode root, int targetSum) {
        getSum(root,targetSum);
        return flag;
    }

    public void getSum(TreeNode root,int targetSum){
        if(root == null){
            return;
        }
        targetSum-=root.val;
        if(targetSum == 0 && root.left == null && root.right == null){
            flag = true;
        }
        getSum(root.left,targetSum);
        getSum(root.right,targetSum);
        targetSum+=root.val;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

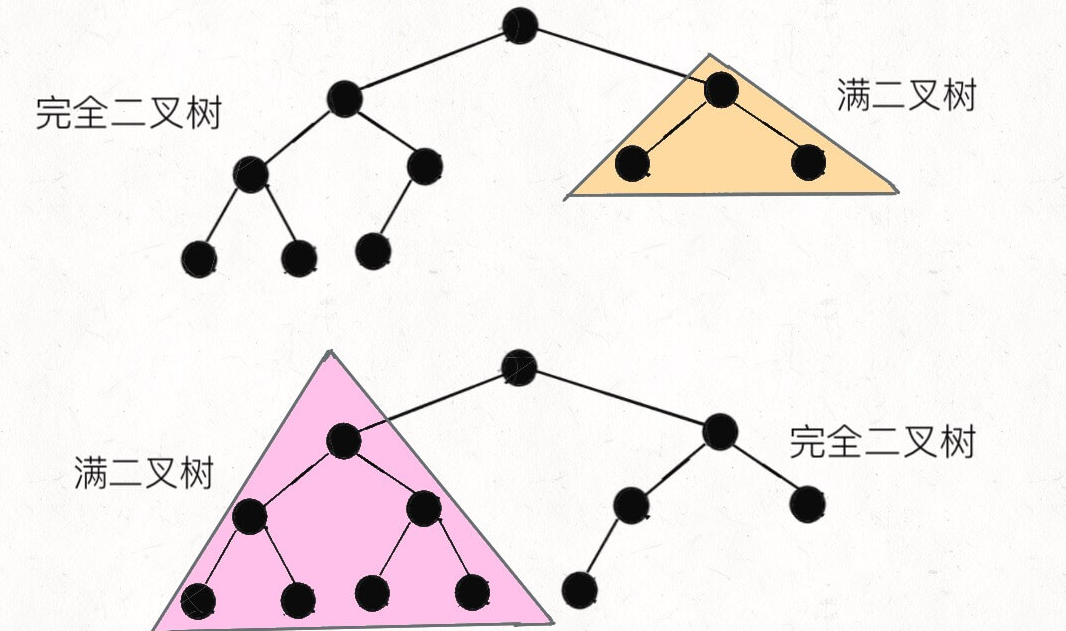
# 15.(`easy`)完全二叉树的结点个数

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2的h次方个节点。

思路：

常规思路，想到遍历二叉树统计结点，但没有利用到完全二叉树的性质，时间复杂度是O(n)

利用完全二叉树的性质，只有最底层的结点可能没填满，那么一直到填满的那一层的所有结点数就可以计算到为：2^h-1，h为填满的层数(高度)，一层1一个结点、二层3个，以此类推，所以我们在递归时，每次找一下当前结点的左右子树的高度，如果左右子树高度一致一样，证明到子树的一层为止，二叉树是满二叉树，就可以用上面的公式计算总结点数，时间复杂度是 O(logN*logN)
时间复杂度为什么是O(logN*logN)呢？

直觉感觉好像最坏情况下是 O(N*logN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：
return 1 + countNodes(root.left) + countNodes(root.right);
1
关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发 hl == hr 而立即返回，不会递归下去。

为什么呢？原因如下：

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：
由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发 hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。

代码：

class Solution {
    public int countNodes(TreeNode root) {
        TreeNode left = root;
        int leftHigh = 0;
        while(left!=null){
            left = left.left;
            leftHigh++;
        }
        TreeNode right = root;
        int rightHigh = 0;
        while(right!=null){
            right = right.right;
            rightHigh++;
        }
        if(leftHigh==rightHigh){
            return (int)Math.pow(2,rightHigh)-1;
        }
        return 1+countNodes(root.left)+countNodes(root.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 16.(`medium`)二叉树中和为某一值的路径

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

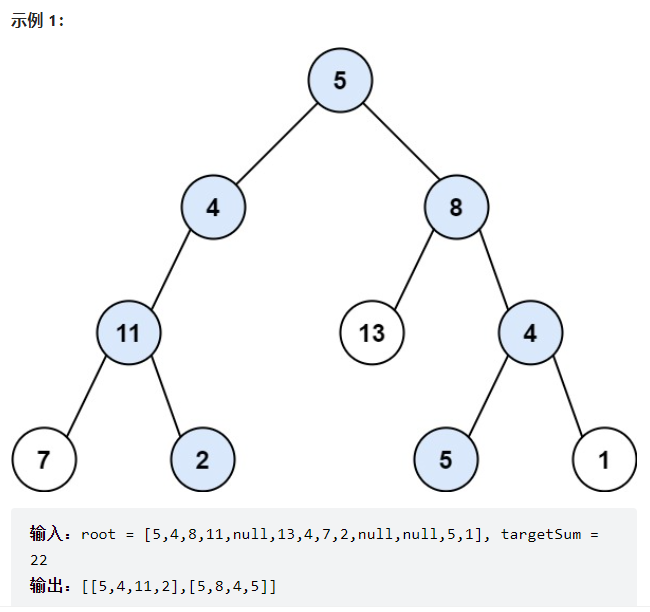
思路：

本问题是典型的二叉树方案搜索问题，使用回溯法解决，其包含 先序遍历 + 路径记录 两部分。

先序遍历时，每次让target减去当前节点值，并把当前节点值加入到路径记录链表path中。

如果此时target==0，且当前节点没有左右子节点(因为题目要求找根节点到叶子结点的和)，那么此时的path中的节点满足要求，将其加入到res数组中去。
res.add(new LinkedList(path));
1
向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.removeLast() 。

值得注意的是，记录路径时若直接执行res.add(path)，则是将path对象加入了res，后续 path改变时，res中的path对象也会随之改变。

正确做法：res.add(new LinkedList(path))，相当于复制了一个path并加入到res 。

代码：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        find(root,target);
        return res;
    }
    public void find(TreeNode root, int target){
        if(root == null){
            return;
        }
        path.add(root.val);
        target-=root.val;
        if(target == 0 && root.left == null && root.right == null){
            res.add(new LinkedList(path));
        }
        find(root.left,target);
        find(root.right,target);
        target+=root.val;
        path.removeLast();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 17.(`medium`)树的子结构(理解不深)

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构，即 A中有出现和B相同的结构和节点值。

例如: 给定的树 A:

3
/ \

4 5 /
1 2 给定的树 B：

4 / 1 返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1] 输出：false 示例 2：

输入：A = [3,4,5,1,2], B = [4,1] 输出：true

思路：

若树B是树A的子结构，则子结构的根节点可能为树A的任意一个节点。因此，判断树B是否是树A的子结构，需要以下两步：

先序遍历树A中的每个节点a(对应函数isSubStructure(A,B))

判断树A中以a为根节点的子树是否包含树B。(对应函数judge(A,B))

judge函数：

终止条件：当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 true；当节点 A 为空：说明已经越过树 A 叶子节点，即匹配失败，返回 false；当节点 A 和 B 的值不同：说明匹配失败，返回 false；

返回值：

判断A和B的左子节点是否相等，即judge(A.left,B.left)

判断A和B的右子节点是否相等，即judge(A.right,B.right)

isSubStructure(A,B)函数：

特例处理：当树A为空或树B为空时，直接返回false；

返回值：若树B是树A的子结构，则必须满足以下三种情况之一，因此用||连接；

以节点A为根节点的子树包含树B，对应judge(A,B)

树B是树A左子树的子结构，对应isSubStructure(A.left,B)

树B是树A右子树的子结构，对应isSubStructure(A.right,B)

以上2、3点实质上是在对树A做先序遍历

复杂度分析：时间复杂度 O(MN)：其中M,N 分别为树 A 和树 B 的节点数量；先序遍历树 A 占用 O(M) ，每次调用 judge(A, B) 判断占用O(N) 。空间复杂度 O(M) ：当树 A 和树 B 都退化为链表时，递归调用深度最大。当 M≤N 时，遍历树 A 与递归判断的总递归深度为 M ；当 M>N 时，最差情况为遍历至树 A 叶子节点，此时总递归深度为 M。

代码：

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(B == null || A == null){
            return false;
        }
        //遍历A中每个节点，A树中任一节点包含B就能返回true
        return judge(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }
    public boolean judge(TreeNode A,TreeNode B){
        if(B == null){
            return true;
        }
        if(A == null||A.val != B.val){
            return false;
        }
        return judge(A.left,B.left)&&judge(A.right,B.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 18.(`medium`)从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如: 给定二叉树: [3,9,20,null,null,15,7],

/
9 20 /
15 7 返回：

[3,9,20,15,7]

思路：

层序遍历

代码：

class Solution {
    public int[] levelOrder(TreeNode root) {
        if(root == null){
            return new int[0];
        }
        List<Integer> res = new ArrayList<>();
        Deque<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            int curLen = queue.size();
            for(int i=0;i<curLen;i++){
                TreeNode cur = queue.pop();
                res.add(cur.val);
                if(cur.left!=null){
                    queue.add(cur.left);
                }
                if(cur.right!=null){
                    queue.add(cur.right);
                }
            }
        }
        int[] nums = new int[res.size()];
        for(int i=0;i<res.size();i++){
            nums[i] = res.get(i);
        }
        return nums;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 19.(`medium`)从上到下打印二叉树3

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如: 给定二叉树: [3,9,20,null,null,15,7],

/
9 20 /
15 7 返回其层次遍历结果：

[[3],[20,9],[15,7]]

思路：

与上题不同的是，temp使用LinkedList，奇数层时，每个curNode的值放到temp的尾部，偶数层放到temp的头部。

这里使用一个boolean的flag表示奇偶

代码：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if(root == null){
            return new ArrayList<>();
        }
        List<List<Integer>> res = new ArrayList<>();
        Deque<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        boolean flag = false; 
        while(!queue.isEmpty()){
            LinkedList<Integer> temp = new LinkedList<>();
            int curLen = queue.size();
            for(int i=0;i<curLen;i++){
                TreeNode cur = queue.pop();
                if(flag){
                    temp.addFirst(cur.val);
                }else{
                    temp.addLast(cur.val);
                }
                if(cur.left!=null){
                    queue.add(cur.left);
                }
                if(cur.right!=null){
                    queue.add(cur.right);
                } 
            }
            flag = !flag;
            res.add(temp);
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 20.(`easy`)平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

/
9 20 /
15 7 返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

1
/ \
2   2
/ \

3 3 /
4 4 返回 false 。

思路：

用一个res记录下返回的boolean，初始化为true，后续遍历求到左右子树的深度，比较一下差值的绝对值是否大于1，大于则更新res为false，并直接返回一个值防止继续递归。主函数中返回res即可

代码：

class Solution {
    boolean res = true;
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        travers(root);
        return res; 
    }

    public int travers(TreeNode root){
        if(root == null){
            return 0;
        }
        int left = travers(root.left);
        int right = travers(root.right);
        if(Math.abs(left-right)>1){
            res = false;
            return 0;
        }
        return Math.max(left,right)+1;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 21.(`easy`)二叉树的最近公共祖先

给定一个二叉树找到该树中两个指定结点的最近公共祖先

思路：

此题的二叉树是普通二叉树不是二叉搜索树，所以无法按二叉搜索树的方法找，不过大体思想是相同的。

如果此时的root结点为null或者p、q中的任何一个，就返回。因为p、q中如果有等于root的，那么p或q本身就是它们的最近公共祖先

然后递归遍历左子树，只要在左子树中找到了p或q，则先找到谁就返回谁

然后递归遍历右子树，只要在右子树中找到了p或q，则先找到谁就返回谁

如果在左子树中 p和 q都找不到，则 p和 q一定都在右子树中，右子树中先遍历到的那个就是最近公共祖先（一个节点也可以是它自己的祖先）

否则，如果 left不为空，在左子树中有找到节点（p或q），这时候要再判断一下右子树中的情况，如果在右子树中，p和q都找不到，则 p和q一定都在左子树中，左子树中先遍历到的那个就是最近公共祖先（一个节点也可以是它自己的祖先）

否则，当 left和 right均不为空时，说明 p、q节点分别在 root异侧, 最近公共祖先即为 root

代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q){
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left == null){
            return right;
        }
        if(right == null){
            return left;
        }
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 二、二叉搜索树BST

BST 相关的问题，要么利用 BST 左小右大的特性提升算法效率，要么利用中序遍历的特性满足题目的要求

# 1.(`easy`)二叉搜索树的第k大结点

给定一棵二叉搜索树，请找出其中第 k 大的节点的值。

示例 1:

输入: root = [3,1,4,null,2], k = 1 3 /
1 4
2 输出: 4 示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3 5 /
3 6 /
2 4 / 1 输出: 4

思路：

因为对二叉搜索树使用中序遍历，得到的是所有结点的升序，而题目要求第K大(不是第K小)，所以使用反序中序遍历(先root.right，再root.left)

# 2.(`medium`)把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：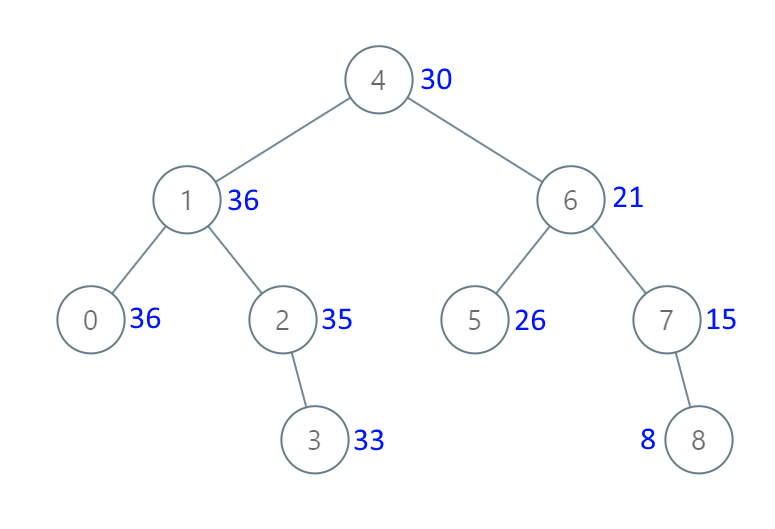

思路：

由于二叉搜索树的特性我们知道，每个结点的右子节点的值总是大于该结点，左子节点的值总是小于该结点，所以我们使用一个sum变量来储存比当前结点值大的结点的累加和，然后当前结点的值就应该等于它本身加上这个sum，然后更新sum为当前结点值。

所以我们需要使用反中序遍历，即先遍历右子结点(因为右子节点才是比当前结点大的)，再遍历左子节点

代码：

class Solution {
    int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root == null){
            return null;
        }
        convertBST(root.right);
        sum += root.val;
        root.val = sum;
        convertBST(root.left);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13

#

# 3.(`medium`)删除二叉搜索树中的结点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；如果找到了，删除它。

示例 1: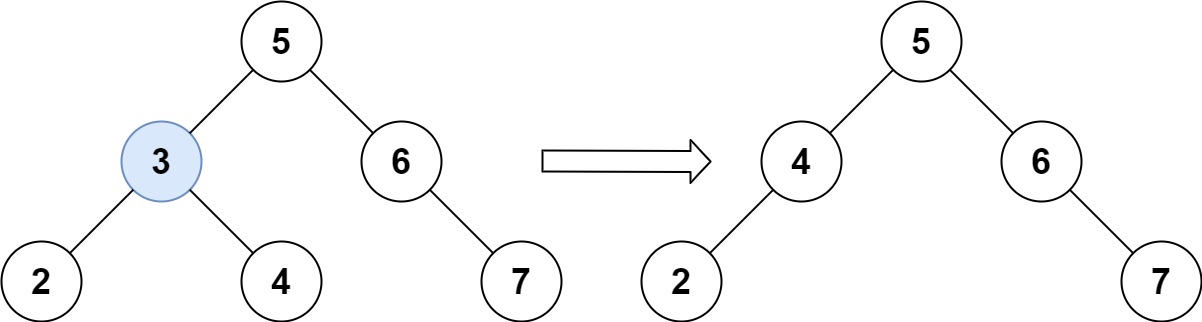

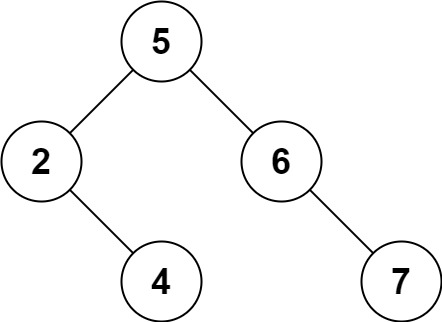
输入：root = [5,3,6,2,4,null,7], key = 3 输出：[5,4,6,2,null,null,7] 解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。另一个正确答案是 [5,2,6,null,4,null,7]。

思路：

找到目标结点后，有三种情况，

目标结点无子节点，直接返回null即可；

左子结点不为null，直接让当前结点root=left左子节点
如果此时右子节点也不为null，那么就需要找到左子节点left的最右子节点(即值最大结点)，然后将右子节点right接到它后面(因为二叉搜索树的性质，右边结点值肯定比左边任何一个大，所以找到左边最大的接上就行)

右子结点不为null，直接让当前结点root=right右子节点
如果此时左子节点也不为null，那么就需要找到右子节点right的最左子节点(即值最小结点)，然后将左子节点left接到它后面(因为二叉搜索树的性质，左边结点值肯定比右边任何一个小，所以找到右边最小的接上就行)

处理完目标结点后，就返回新的结点，此时需要特判一下

如果此时的结点为null了，就不能对它的left、right赋值

此时结点不为null，因为返回时处理后的新结点，比如例一中，原本是3，现在返回的是2，但是原来的5的left仍然连着3，所以我们需要让5的left指向2，所以有root.left = 返回值；同理如果要找的结点在右子树上，有root.right = 返回值。

代码：

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null){
            return null;
        }
        if(root.val == key){
            TreeNode left = root.left;
            TreeNode right = root.right;
            if(left != null){
                root = left;
                if(right!=null){
                    TreeNode p = root;
                    while(p.right != null){
                        p = p.right;
                    }
                    p.right = right;
                }
            }else if(right != null){
                root = right;
                if(left!=null){
                    TreeNode p = root;
                    while(p.left != null){
                        p = p.left;
                    }
                    p.left = left;
                }
            }else if(left==null&&right==null){
                root = null;
            }
        }
        if(root != null){
            root.left = deleteNode(root.left,key);
            root.right = deleteNode(root.right,key);
        }
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#

# 4.(`easy`)二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

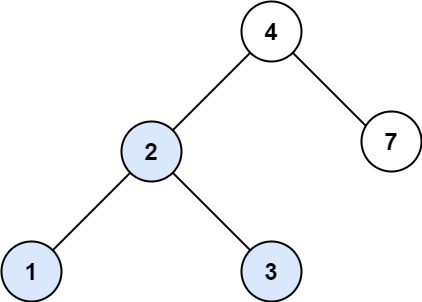
输入：root = [4,2,7,1,3], val = 2 输出：[2,1,3]

思路：

在非BST中，我们每次都要遍历左右子树去搜索某个结点，而在BST中，基于它的性质，我们可以根据当前结点的值与要寻找的值的大小比较，来决定去左子树搜索还是去右子树搜索，类似二分查找，提高了效率

代码：

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null){
            return null;
        }
        if(val>root.val){
            return searchBST(root.right,val);
        }
        if(val<root.val){
            return searchBST(root.left,val);
        }
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 5.(`medium`)验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例1

 2
  / \
 1   3

输入：root = [2,1,3]
输出：true

1
2

示例2

  5
  / \
 1   4

/ \

3 6

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

1
2
3

思路：

利用BST的中序遍历得到的是结点值升序，只需使用一个preValue变量保存中序遍历中前一个结点的值，与现在的root.val相比较，如果root.val<preValue，则表示不是BST；每次比较完后，用当前结点值更新preValue

代码：

class Solution {
    long preValue = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        //为null直接返回true
        if(root == null){
            return true;
        }
        //如果左子节点不满足 直接false
        if(!isValidBST(root.left)){
            return false;
        }
        //如果当前结点值比上一个小 不满足 false
        if(root.val<=preValue){
            return false;
        }
        //更新上一个结点值为当前结点值
        preValue = root.val;
        //判断右子节点是否满足
        return isValidBST(root.right);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 6.(`medium`)二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

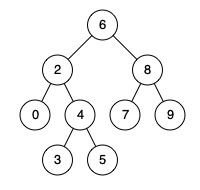
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

思路：

根据二叉搜索树的性质，

若root是p,q的最近公共祖先则只可能为以下情况之一：

p和q在root的子树中，且分列root的异侧(即分别在左、右子树中)；

p=root，且q在root的左或右子树中；

q=root，且p在root的左或右子树中；

举个例子，当前节点(10)同时大于p(3)、q(5)两节点的值，那么pq肯定在当前节点的左子树上，然后当前节点移动到6，

6仍然都比pq大，pq在6的左子树上，当前节点移动到4,4在pq之间，所以4是最近公共祖先

10

/ \

6 13

/ \

4 8

/ \

3 5

代码：

使用递归

当pq并不都在当前节点的一边时，即pq位置出现了分叉，证明当前的节点就是pq的最近公共祖先

class Solution {
 	public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p.val<root.val && q.val<root.val){
            return lowestCommonAncestor(root.left,p,q);
        }else if(p.val>root.val && q.val>root.val){
            return lowestCommonAncestor(root.right,p,q);
        }
        return root;
    }   
}

1
2
3
4
5
6
7
8
9
10

使用迭代

class Solution {
 	public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while(root!=null){
            if(p.val<root.val && q.val<root.val){
                root = root.left;
            }
            else if(p.val>root.val && q.val>root.val){
                root = root.right;
            }else{
                break;
            }
        }
        return root;
    }  
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 三、二叉树递归转迭代

# 迭代遍历二叉树的代码框架

// 模拟函数调用栈
private Stack<TreeNode> stk = new Stack<>();

// 左侧树枝一撸到底
private void pushLeftBranch(TreeNode p) {
    while (p != null) {
        /*******************/
        /** 前序遍历代码位置 **/
        /*******************/
        stk.push(p);
        p = p.left;
    }
}

public List<Integer> traverse(TreeNode root) {
    // 指向上一次遍历完的子树根节点
    TreeNode visited = new TreeNode(-1);
    // 开始遍历整棵树
    pushLeftBranch(root);
    
    while (!stk.isEmpty()) {
        TreeNode p = stk.peek();
        
        // p 的左子树被遍历完了，且右子树没有被遍历过
        if ((p.left == null || p.left == visited) 
          && p.right != visited) {
            /*******************/
            /** 中序遍历代码位置 **/
            /*******************/
            // 去遍历 p 的右子树
            pushLeftBranch(p.right);
        }
        // p 的右子树被遍历完了
        if (p.right == null || p.right == visited) {
            /*******************/
            /** 后序遍历代码位置 **/
            /*******************/
            // 以 p 为根的子树被遍历完了，出栈
            // visited 指针指向 p
            visited = stk.pop();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

代码中最有技巧性的是这个 visited 指针，它记录最近一次遍历完的子树根节点（最近一次 pop 出栈的节点），我们可以根据对比 p 的左右指针和 visited 是否相同来判断节点 p 的左右子树是否被遍历过，进而分离出前中后序的代码位置。

PS：visited 指针初始化指向一个新 new 出来的二叉树节点，相当于一个特殊值，目的是避免和输入二叉树中的节点重复。

只需把递归算法中的前中后序位置的代码复制粘贴到上述框架的对应位置，就可以把任意递归的二叉树算法改写成迭代形式了。

# 四、根据遍历结果还原二叉树

# 1.(`medium`)重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例1：

[3,9,20,15,7] [9,3,15,20,7]

/ \

9 20

/ \

15 7

输出：[3,9,20,null,null,15,7]

思路：

从前序遍历和中序遍历的特点，我们可以得出以下信息：

前序遍历数组的preorder[0]肯定是原整棵树的根节点

而在在中序遍历数组inorder中，已这个perorder[0]值为界限，将数组分成左右两部分，分别是原树的左子树的所有结点和右子树的所有结点

因为

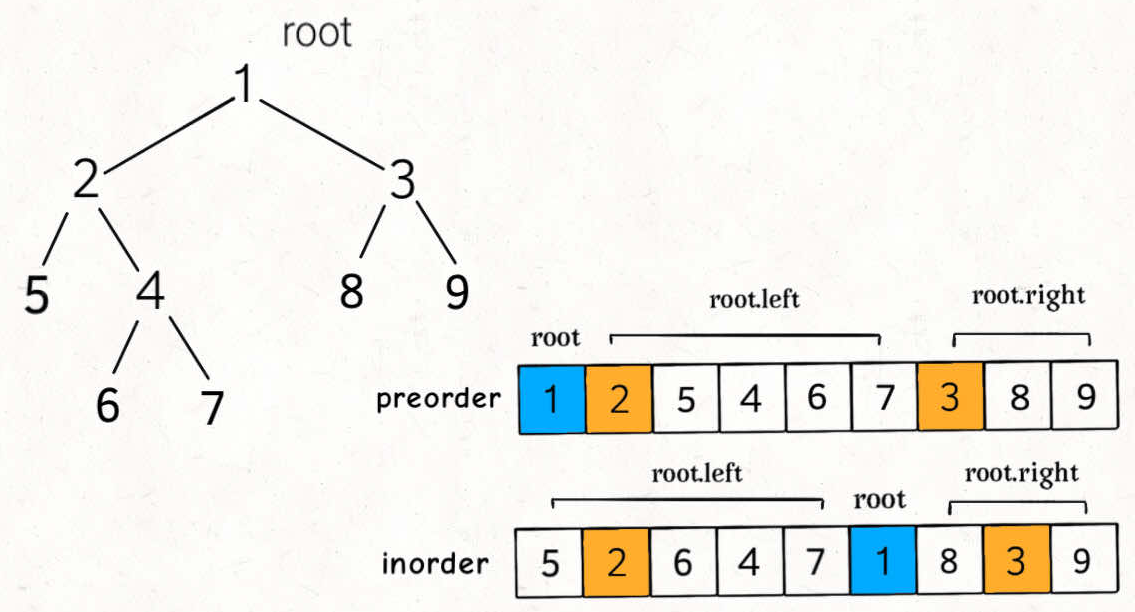
对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ] 即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

在中序遍历数组中对根节点进行定位时，由于结点的值是不重复的，可以使用HashMap取代for循环查找来快速得到根节点的索引位置，从而降低时间复杂度

代码：

class Solution {
    int[] preorder;
    Map<Integer,Integer> indexMap = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for(int i=0;i<inorder.length;i++){
            indexMap.put(inorder[i],i);
        }
        return build(0,0,inorder.length-1);
    }

    public TreeNode build(int rootIndex,int leftIndex,int rightIndex){
        if(leftIndex>rightIndex){
            return null;
        }
        TreeNode root = new TreeNode(preorder[rootIndex]);
        int boundIndex = indexMap.get(preorder[rootIndex]);
        //当前根节点的左子树在中序遍历数组中的区间[leftIndex,boundIndex-1]
        //左子树的根节点位置为：从前序遍历数组0开始每次+1
        root.left = build(rootIndex+1,leftIndex,boundIndex-1);
        //当前根节点的右子树在中序遍历数组中的区间[boundIndex+1,rightIndex]
        //右子树的根节点为 根节点索引 + 左子树长度 + 1
        root.right = build(rootIndex+(boundIndex-leftIndex+1),boundIndex+1,rightIndex);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

在 GitHub 上编辑此页

#二叉树 #算法

最后更新: 2022/10/04, 16:10:00

← 纲要链表→

二叉树

# 递归

# 二叉树遍历框架

# 其他数据结构的遍历

# 重点

# 一、普通二叉树

# 1.(easy)二叉树的前序遍历

# 2.(easy)二叉树的深度

# 3.(easy)翻转二叉树

# 4.(medium)二叉树的层序遍历

# 5.(medium)N叉树的层序遍历

# 6.(medium)填充每个结点的下一个右侧结点指针

# 7.(easy)二叉树的直径

# 8.(easy)对称二叉树

# 9.(easy) 合并二叉树

# 10.(medium)二叉树展开为链表

# 11.(medium)最大二叉树

# 12.(medium)寻找重复的子树

# 13.(easy)二叉树的镜像

# 14.(easy)路径总和

# 15.(easy)完全二叉树的结点个数

# 16.(medium)二叉树中和为某一值的路径

# 17.(medium)树的子结构(理解不深)

# 18.(medium)从上到下打印二叉树

# 19.(medium)从上到下打印二叉树3

# 20.(easy)平衡二叉树

# 21.(easy)二叉树的最近公共祖先

# 二、二叉搜索树BST

# 1.(easy)二叉搜索树的第k大结点

# 2.(medium)把二叉搜索树转换为累加树

#

# 3.(medium)删除二叉搜索树中的结点

#

# 4.(easy)二叉搜索树中的搜索

# 5.(medium)验证二叉搜索树

# 6.(medium)二叉搜索树的最近公共祖先

# 三、二叉树递归转迭代

# 迭代遍历二叉树的代码框架

# 四、根据遍历结果还原二叉树

# 1.(medium)重建二叉树

# 1.(`easy`)二叉树的前序遍历

# 2.(`easy`)二叉树的深度

# 3.(`easy`)翻转二叉树

# 4.(`medium`)二叉树的层序遍历

# 5.(`medium`)N叉树的层序遍历

# 6.(`medium`)填充每个结点的下一个右侧结点指针

# 7.(`easy`)二叉树的直径

# 8.(`easy`)对称二叉树

# 9.(`easy`) 合并二叉树

# 10.(`medium`)二叉树展开为链表

# 11.(`medium`)最大二叉树

# 12.(`medium`)寻找重复的子树

# 13.(`easy`)二叉树的镜像

# 14.(`easy`)路径总和

# 15.(`easy`)完全二叉树的结点个数

# 16.(`medium`)二叉树中和为某一值的路径

# 17.(`medium`)树的子结构(理解不深)

# 18.(`medium`)从上到下打印二叉树

# 19.(`medium`)从上到下打印二叉树3

# 20.(`easy`)平衡二叉树

# 21.(`easy`)二叉树的最近公共祖先

# 1.(`easy`)二叉搜索树的第k大结点

# 2.(`medium`)把二叉搜索树转换为累加树

# 3.(`medium`)删除二叉搜索树中的结点

# 4.(`easy`)二叉搜索树中的搜索

# 5.(`medium`)验证二叉搜索树

# 6.(`medium`)二叉搜索树的最近公共祖先

# 1.(`medium`)重建二叉树