排序
排序
Table of Contents generated with DocToc (opens new window)
# 选择排序
# 思路:
每一轮选出未排序部分中最小的元素交换到未排序部分的最开头。即:
先选出最小的,再选出第二小的,以此类推。
# 代码
/**
* @author zdk
* @date 2022/3/27 10:43
* 选择排序
*/
public class SelectSort {
/**
* 每一轮选取未排定的部分中最小的元素交换到未排定部分的最开头
* 即:先选出最小的,再选出第 2 小的,以此类推。
* @param nums
*/
public void selectSort(int[] nums){
for (int i = 0; i < nums.length-1; i++) {
int minIndex = i;
for (int j = i+1; j < nums.length; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
swap(nums, i, minIndex);
}
}
public void swap(int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
@Test
public void test(){
int[] nums = new int[]{5,6,2,1,9,8};
selectSort(nums);
System.out.println(Arrays.toString(nums));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 总结:
- 算法思想1:贪心算法。每一此决策只看当前,当前最优,则全局最优。注意:这种思想不是任何时候都适用
- 算法思想 2:减治思想:外层循环每一次都能排定一个元素,问题的规模逐渐减少,直到全部解决,即「大而化小,小而化了」。运用「减治思想」很典型的算法就是大名鼎鼎的「二分查找」。
- 优点:交换次数最少。
# 复杂度分析:
- 时间复杂度:O(N^2),这里N是数组的长度;
- 空间复杂度:O(1),使用到常数个临时变量。
# 插入排序
# 思路:
每次比较当前下标j的数是否小于前一个j-1,如果小于,就将其移动到[0,j)这个区间中,小于这个数的位置之前。
比如5 2 6 4 3,第一次移动 变成 2 5 6 4 3,第二次nums[j]==4,此时将4移动到小于它的数的前面,即2前面,所以数组变成 2 4 5 6 3,最后将3移动到2前面,2 3 4 5 6,排序完成
# 代码:
public void insertSort(int[] nums){
for (int i = 0; i < nums.length; i++) {
//移动过程相当于前面的数组整体向前移动一位,最后一个数移动到开头
//所以用temp来记录最后一个数
//然后让每个数等于它前面的数,再循环即可
int temp = nums[i];
int j = i;
while (j>0 && nums[j-1]>temp) {
nums[j] = nums[j-1];
j--;
}
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# 总结:
特点:
「插入排序」可以提前终止内层循环(体现在 nums[j - 1] > temp 不满足时),在数组「几乎有序」的前提下,「插入排序」的时间复杂度可以达到 O(N)
由于「插入排序」在「几乎有序」的数组上表现良好,特别地,在「短数组」上的表现也很好。因为「短数组」的特点是:每个元素离它最终排定的位置都不会太远。为此,在小区间内执行排序任务的时候,可以转向使用「插入排序」。
# 复杂度分析:
- 时间复杂度:O(N^2),这里N是数组的长度;
- 空间复杂度:O(1),使用到常数个临时变量。
# 冒泡排序
# 思路:
- 基本思想:外层循环每一次经过两两比较,把每一轮未排定部分最大的元素放到了数组的末尾;
- 「冒泡排序」有个特点:在遍历的过程中,提前检测到数组是有序的,从而结束排序,而不像「选择排序」那样,即使输入数据是有序的,「选择排序」依然需要「傻乎乎」地走完所有的流程。
# 代码:
public void bubblingSort(int[] nums){
for (int i = nums.length-1; i >= 0; i--) {
// 先默认数组是有序的,只要发生一次交换,就必须进行下一轮比较,
// 如果在内层循环中,都没有执行一次交换操作,说明此时数组已经是升序数组
boolean sorted = true;
for (int j = 0; j < i; j++) {
if (nums[j]>nums[j+1]) {
swap(nums, j,j+1);
sorted = false;
}
}
if (sorted){
break;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 归并排序
# 代码框架
// 定义:排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = (lo + hi) / 2;
// 利用定义,排序 nums[lo..mid]
sort(nums, lo, mid);
// 利用定义,排序 nums[mid+1..hi]
sort(nums, mid + 1, hi);
/****** 后序位置 ******/
// 此时两部分子数组已经被排好序
// 合并两个有序数组,使 nums[lo..hi] 有序
merge(nums, lo, mid, hi);
/*********************/
}
// 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
// 合并为有序数组 nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 代码实现
public class MergeSort {
int[] temp;
public void mergeSort(int[] nums){
temp = new int[nums.length];
sort(nums, 0, nums.length-1);
}
public void sort(int[] nums, int low,int high){
if (low == high){
return;
}
int mid = low + (high-low) / 2;
sort(nums, low, mid);
sort(nums, mid+1, high);
// 如果数组的这个子区间本身有序,无需合并
if (nums[mid] <= nums[mid + 1]) {
return;
}
merge(nums, low, mid, high);
}
public void merge(int[] nums, int low,int mid,int high){
//把值复制到临时数组temp 再合并回去
System.arraycopy(nums, low, temp, low, high + 1 - low);
//双指针对两个排序数组 进行合并
//两个指针 分别指向两个数组的开头
int i = low,j = mid+1;
for (int k = low; k <= high; k++) {
//左边的排序完了
if (i == mid+1){
nums[k] = temp[j++];
}else if (j == high+1){
nums[k] = temp[i++];
}else if (temp[i]<=temp[j]){
// 注意写成 < 就丢失了稳定性(相同元素原来靠前的排序以后依然靠前)
nums[k] = temp[i++];
}else{
nums[k] = temp[j++];
}
}
}
@Test
public void test(){
int[] nums = new int[]{5,6,2,1,9,8};
mergeSort(nums);
System.out.println(Arrays.toString(nums));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
优化1:sort方法中,在两个数组本身就是有序的情况下,无需合并
if (nums[mid] <= nums[mid + 1]) return;1优化2:
全程使用一份临时数组进行合并两个有序数组的操作,避免创建临时数组和销毁的消耗,避免计算下标偏移量注意:实现归并排序的时候,不要把算法实现成非稳定排序,区别在于<=和<
「归并排序」比「快速排序」好的一点是,它借助了额外空间,可以实现「稳定排序」
# 复杂度分析
- 时间复杂度:O(NlogN),这里N是数组的长度;
- 空间复杂度:O(N),辅助数组与输入数组规模相当。
# 快速排序
# 思路1:只移动partition指针
初始化partition指针的位置为随机后的数组的第一个元素位置。
当往前遍历发现有一个元素小于基准值时,就将partition指针+1,并将这个元素与nums[partition+1]的值交换
循环完成后把基准值nums[left]与它所应该在的位置的值交换
swap(nums,left,partition),即:让基准值回到它最后的位置(位置左边全是小于基准值的数 右边全是大于基准值的数)
# 代码1:
{
// 快速排序 1:基本快速排序
/**
* 列表大小等于或小于该大小,将优先于 quickSort 使用插入排序
*/
private static final int INSERTION_SORT_THRESHOLD = 7;
public int[] sortArray(int[] nums) {
int len = nums.length;
quickSort(nums, 0, len - 1);
return nums;
}
private void quickSort(int[] nums, int left, int right) {
// 小区间使用插入排序
//如果小区间不使用排序而直接用快排 就会出现求随机partitionIndex时 bound<0的异常
if (right - left <= INSERTION_SORT_THRESHOLD) {
insertionSort(nums, left, right);
return;
}
int pIndex = partition(nums, left, right);
quickSort(nums, left, pIndex - 1);
quickSort(nums, pIndex + 1, right);
}
/**
* 对数组 nums 的子区间 [left, right] 使用插入排序
*
* @param nums 给定数组
* @param left 左边界,能取到
* @param right 右边界,能取到
*/
private void insertionSort(int[] nums, int left, int right) {
for (int i = left + 1; i <= right; i++) {
int temp = nums[i];
int j = i;
while (j > left && nums[j - 1] > temp) {
nums[j] = nums[j - 1];
j--;
}
nums[j] = temp;
}
}
private int partition(int[] nums, int left, int right) {
int randomIndex = new Random().nextInt(right - left + 1) + left;
swap(nums, left, randomIndex);
// 基准值
int pivot = nums[left];
//基准值应该在的位置下标 每次出现小于基准值的数时
//基准值的位置+1 并将该值与+1后的基准值位置的元素交换
int partition = left;
for (int i = left + 1; i <= right; i++) {
if (nums[i] < pivot) {
partition++;
swap(nums, i, partition);
}
}
//让基准值回到它最后的位置(位置左边全是小于基准值的数 右边全是大于基准值的数)
swap(nums, left, partition);
return partition;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
@Test
public void test(){
int[] nums = new int[]{5,6,2,1,9,8,7,0,3,4};
System.out.println(Arrays.toString(sortArray(nums)));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# 思路2:使用双指针双向移动(更易理解)
依然使用随机数来确定基准值的位置,并将基准值交换到要排序的区间的最左边。
然后在左右指针ij未相遇的情况下进行循环
必须先让右指针移动,找到一个小于基准值的位置就停下
(除初次外) 上轮循环结束后,有: nums[i] < pivot , nums[j] > pivot,而如果先进行左移的操作,如果因为 i >= j 跳出,那此时 nums[i] = nums[j] > pivot,就不符合要求了移动右指针、左指针,当右指针找到小于基准值的位置停下,左指针找到大于基准值的位置停下,然后交换两个指针所指位置的值,直到相遇
当指针相遇以后 更新基准值(原为left)的位置到相遇点(i)
递归对[left,i-1]和[i+1,right]区间的数组进行快排(
i即是当前区间数组中的基准值所在的位置)
# 代码2:
class Solution {
public int[] sortArray(int[] nums) {
quickSort(nums,0,nums.length-1);
return nums;
}
public void quickSort(int[] nums, int left, int right) {
if(left>right){
return;
}
//使用随机获取基准值 防止出现极端情况
//极端情况会退化为冒泡
int randomIndex = new Random().nextInt(right-left+1)+left;
swap(nums,randomIndex,left);
int pivot = nums[left];
int i = left,j = right;
while(i!=j){
//必须先执行 从右往左遍历
while(i<j && nums[j]>=pivot){
j--;
}
while(i<j && nums[i]<=pivot){
i++;
}
//找到了右边小于基准值 左边大于基准值的时候 交换
swap(nums,i,j);
}
//当指针相遇以后 更新基准值(原为left)的位置到相遇点(i)
swap(nums,left,i);
quickSort(nums, left, i - 1);
quickSort(nums, i + 1, right);
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 计数排序
# 思路:
对数组A进行排序,使用一个数组temp,初始化temp的下标为A的值,temp[i]为这个值出现的次数- 在上面的过程中,我们可以先对A遍历一次,拿到A中的最大最小值,用最大值确定temp的容量大小,为
max+1- 然后就可以用我们想要的方式遍历数组,获得排序后的结果等等
特别注意:当数组中有负数时,为了保证下标为>=0,所以需要给temp的每个下标增加上一个offset偏移量,其值为规定的abs(题目规定的最小值)
# 代码:
public class CountSort {
//防止负数的偏移量
int offset = 0;
public int[] countSort(int[] nums){
int max = nums[0];
int min = nums[0];
for (int num : nums) {
max = Math.max(max,num);
min = Math.min(min,num);
}
//temp数组
int[] temp = new int[max + 1 + offset];
max+=offset;
min+=offset;
//初始化temp
for (int num : nums) {
temp[num+offset]++;
}
int[] res = new int[nums.length];
int index = 0;
for (int i=min;i<=max;i++) {
for (int j = 0; j < temp[i]; j++) {
res[index++] = i-offset;
}
}
return res;
}
@Test
public void test(){
int[] nums = new int[]{5,6,2,1,9,8,156,2,165,3,1651,20,62,15,30,84,11,0};
System.out.println(Arrays.toString(countSort(nums)));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 题目
# 1.(medium)排序数组
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5] 示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
# 使用归并排序
归并排序是将数组每次递归拆分为两个部分,对这两个部分进行排序后,再将这两个已排序的数组合并(方法类似合并两个有序链表),按此步骤递归即可
代码:
class Solution {
int[] temp;
public int[] sortArray(int[] nums) {
temp = new int[nums.length];
sort(nums,0,nums.length-1);
return nums;
}
public void sort(int[] nums,int low,int high){
if(low == high){
return;
}
int mid = low+(high-low)/2;
sort(nums,low,mid);
sort(nums,mid+1,high);
merge(nums,low,mid,high);
}
public void merge(int[] nums,int low,int mid,int high){
for(int i=low;i<=high;i++){
temp[i] = nums[i];
}
//与双指针合并两个有序链表类似
int i = low,j = mid+1;
for(int k=low;k<=high;k++){
if(i == mid+1){
//此时左边部分数组已全部被合并,所以当前的num[k]的值应该等于当前的j所在位置的值
//即该等于右边部分数组的指针位置的值
nums[k] = temp[j++];
}else if(j == high+1){
//类似上面 此时右边部分数组已全部被合并
nums[k] = temp[i++];
}else if(temp[i]<temp[j]){
nums[k] = temp[i++];
}else{
nums[k] = temp[j++];
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
另一种写法:不适用merge函数,直接将逻辑写到后序代码位置对数组进行处理
class Solution {
int[] temp;
public int[] sortArray(int[] nums) {
temp = new int[nums.length];
sort(nums,0,nums.length-1);
return nums;
}
public void sort(int[] nums,int low,int high){
if(low == high){
return;
}
int mid = low+(high-low)/2;
sort(nums,low,mid);
sort(nums,mid+1,high);
for(int i=low;i<=high;i++){
temp[i] = nums[i];
}
int i = low,j = mid+1;
for(int k=low;k<=high;k++){
if(i == mid+1){
nums[k] = temp[j++];
}else if(j == high+1){
nums[k] = temp[i++];
}else if(temp[i]<temp[j]){
nums[k] = temp[i++];
}else{
nums[k] = temp[j++];
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 时间复杂度分析
递归算法的复杂度计算,就是子问题个数 x 解决一个子问题的复杂度。对于归并排序来说,时间复杂度显然集中在
merge函数遍历nums[lo..hi]的过程,但每次merge输入的lo和hi都不同,所以不容易直观地看出时间复杂度。
merge函数到底执行了多少次?每次执行的时间复杂度是多少?总的时间复杂度是多少?
执行的次数是二叉树结点的个数,每次执行的复杂度就是每个结点代表的子数组的长度,所以总的时间复杂度就是整棵树中数组元素的个数。所以从整体是哪个看,这个二叉树的高度是logN,其中每一层的元素个数就是原数组的长度N,所以总的时间复杂度就是
O(NlogN)。
# 使用计数排序
思路上面有写,注意为负数时要增加offset偏移量即可
代码:
class Solution {
public int[] sortArray(int[] nums) {
return countSort(nums);
}
public int[] countSort(int[] nums){
int max = nums[0];
int min = nums[0];
for (int num : nums) {
max = Math.max(max,num);
min = Math.min(min,num);
}
max+=50000;
min+=50000;
//temp数组
int[] temp = new int[max + 1+50000];
//初始化temp
for (int num : nums) {
temp[num+50000]++;
}
int[] res = new int[nums.length];
int index = 0;
for (int i=min;i<=max;i++) {
for (int j = 0; j < temp[i]; j++) {
res[index++] = i-50000;
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 2.(easy)合并两个有序数组
思路1:采用归并排序中的思想
参考归并排序中合并两个有序数组的方式(类似于合并两个有序链表),借助额外空间,合并两个有序数组,得到更长的有序数组。使用双指针
代码:
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int[] temp = new int[m+n];
int i = 0,j = 0,index = 0;
while(i<m || j<n){
if(i>=m){
temp[index++] = nums2[j++];
}else if(j>=n){
temp[index++] = nums1[i++];
}else if(nums1[i]<=nums2[j]){
temp[index++] = nums1[i++];
}else{
temp[index++] = nums2[j++];
}
}
for(int k=0;k<m+n;k++){
nums1[k] = temp[k];
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 3.(medium)数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
# 方式一:利用快排特性
思路1:
在快排中,我们对每个元素进行划分位置,
每次递归都将其放置到它在排序后数组中的位置上,如果每次递归后,基准值所在下标为i,就表示有i-1个比nums[i]小的值,所以如果i==nums.length-k的话,nums[i]就是排序后数组中第k大的值了。而且可以根据每次递归的i来决定是要对右半区间进行递归还是左半区间进行递归,因为如果此时i<nums.length-k,证明第k大的数的下标肯定在i的右边,所以只需要递归右半部分区间即可,> 时同理
代码:
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSort(nums,0,nums.length-1,nums.length-k);
}
public int quickSort(int[] nums,int left,int right,int index){
if(left>right){
return 0;
}
//随机找基准值防止极端情况
int baseIndex = new Random().nextInt(right-left+1)+left;
swap(nums,left,baseIndex);
int baseValue = nums[left];
//先左后右
int i = left,j = right;
while(i!=j){
//右指针找小于基准值的数
while(i<j && nums[j]>=baseValue){
j--;
}
//左指针找大于基准值的数
while(i<j && nums[i]<=baseValue){
i++;
}
//找到后两指针交换值
swap(nums,i,j);
}
//循环结束后 更新基准值的位置
swap(nums,left,i);
//如果当前的基准值位置即为数组倒数第K的数的下标 即nums.length-k时
//因为此时下标i之前的数都小于nums[i],所以此时的num[i]即为排序后数组第k大的元素
if(i == index){
return nums[i];
}
//递归快排
//如果当前的i小于我们要的下标 证明需要的下标肯定在右半部分数组 反之亦然
//所以只用递归一边的数组快排即可
return i<index ? quickSort(nums,i+1,right,index) : quickSort(nums,left,i-1,index);
}
public void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
思路2:更容易理解
既然要求升序数组中第K大,即为降序数组第K-1个数,将升序快排改一下即可。
如果在当前降序数组中,基准值位置k-1时,nums[i]即为第k大元素,因为此时下标i之前的数都大于nums[i],所以此时的num[i]即为降序排序后数组第k大的元素//将要寻找的下标改成k-1 return quickSort(nums,0,nums.length-1,k-1); //右指针找大于基准值的数(与升序排序相反) while(i<j && nums[j]<=baseValue){ j--; } //左指针找小于基准值的数(与升序排序相反) while(i<j && nums[i]>=baseValue){ i++; }1
2
3
4
5
6
7
8
9
10
11
代码:
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSort(nums,0,nums.length-1,k-1);
}
public int quickSort(int[] nums,int left,int right,int index){
if(left>right){
return 0;
}
int baseIndex = new Random().nextInt(right-left+1)+left;
swap(nums,left,baseIndex);
int baseValue = nums[left];
//先左后右
int i = left,j = right;
while(i!=j){
//右指针找大于基准值的数
while(i<j && nums[j]<=baseValue){
j--;
}
//左指针找小于基准值的数
while(i<j && nums[i]>=baseValue){
i++;
}
//找到后两指针交换值
swap(nums,i,j);
}
swap(nums,left,i);
//如果在当前降序数组中,基准值位置k-1时,nums[i]即为第k大元素
//因为此时下标i之前的数都大于nums[i],所以此时的num[i]即为降序排序后数组第k大的元素
if(i == index){
return nums[i];
}
//递归快排
//如果当前的i小于我们要的下标 证明需要的下标肯定在右半部分数组 反之亦然
//所以只用递归一边的数组快排即可
return i<index ? quickSort(nums,i+1,right,index) : quickSort(nums,left,i-1,index);
}
public void swap(int[] nums,int i,int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 方式二:利用堆排序
# 4.(easy)数组相对排序
给定两个数组,arr1 和 arr2,
arr2 中的元素各不相同 arr2 中的每个元素都出现在 arr1 中 对 arr1 中的元素进行排序,使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。
示例:
输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6] 输出:[2,2,2,1,4,3,3,9,6,7,19]
提示:
1 <= arr1.length, arr2.length <= 1000 0 <= arr1[i], arr2[i] <= 1000 arr2 中的元素 arr2[i] 各不相同 arr2 中的每个元素 arr2[i] 都出现在 arr1 中
思路:
由题意可知arr2中的元素都是不同的,而arr1中可能有重复元素,题目要求将arr1进行排序,但是只要是在arr2中的元素,其相对于其他arr2中的元素的相对位置不能改变,所以我们的思路是先将所有arr2中的元素依顺序全部拿出放到res数组中,再将arr2中没有的元素放到后面,所以使用计数排序。
使用一个temp数组,其下标就是arr1中的元素值,而其值就是arr1中元素出现的次数。在这个过程中,我们通过一次遍历找到arr1的最大最小值,用最大值+1充当temp数组的长度- 先把arr2中的元素放入res:只需要循环arr2,用每个值num为下标找到出现次数,然后res[index++] = num即可。注意:
为了下一步放入非arr2数字,我们需要把添加后的数字的数量重置为0:temp[num]=0,这样下一步每次循环判断一下temp[xx]是不是0即可知道需不需要放入res了- 因为前面求到了最大最小值,所以放入非arr2元素时,不用从0开始循环,直接从min开始,<=max范围即可
代码:
class Solution {
public int[] relativeSortArray(int[] arr1, int[] arr2) {
//找到最大最小值
int max = arr1[0];
int min = arr1[0];
for(int i=0;i<arr1.length;i++){
max = Math.max(max,arr1[i]);
min = Math.min(min,arr1[i]);
}
int[] temp = new int[max+1];
int[] res = new int[arr1.length];
int index = 0;
//统计各个数出现的个数
for(int num:arr1){
temp[num]++;
}
//把arr2中的数先加到res数组中去
for(int num:arr2){
for(int i=0;i<temp[num];i++){
res[index++] = num;
}
//每个数加完以后把个数清零
temp[num] = 0;
}
//把不在arr2中的数加到res数组
for(int i=min;i<=max;i++){
if(temp[i]>0){
for(int j=0;j<temp[i];j++){
res[index++] = i;
}
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
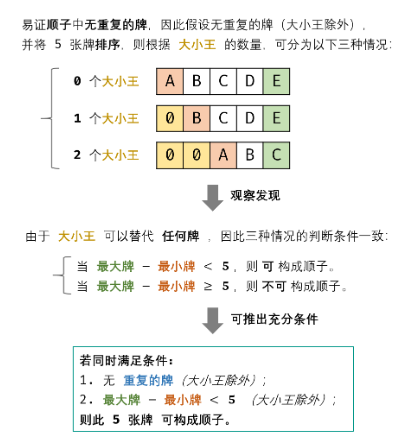
# 5.(easy)扑克牌中的顺子
从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
示例 1:
输入: [1,2,3,4,5]
输出: True
2
示例 2:
输入: [0,0,1,2,5]
输出: True
2
代码:
class Solution {
public boolean isStraight(int[] nums) {
Arrays.sort(nums);
int count = 0;
for(int i=0;i<4;i++){
if(nums[i] == 0){
count++;
continue;
}
//除开大小王 有重复 直接false
if(nums[i+1]==nums[i]){
return false;
}
}
//大小王前的值 如果非0的最小值与最大值相差>=5 就不能构成
return nums[4]-nums[count]<5;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 6.(easy)最小的K个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1] 示例 2:
输入:arr = [0,1,2,1], k = 1 输出:[0]
限制:0 <= k <= arr.length <= 10000;0 <= arr[i] <= 10000
思路:
基于快排的划分方法,进行一次快排后,数组左指针i前面,有i-1个比它小的数了,如果i==k,那么[0,i]这个区间的数就是答案。
如果i<k,证明需要的i更大,所以递归右边数组快排,如果i>k,证明需要的i更小,递归左边数组。
此题与3.数组中的第K个最大元素类似
代码:
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
//特判 有一个特殊用例 k大于了arr的长度,所以直接返回arr即可,否则会返回全0的数组
if(k>=arr.length){
return arr;
}
return quickSort(arr,0,arr.length-1,k);
}
public int[] quickSort(int[] arr,int left,int right,int k){
if(left > right){
return new int[k];
}
//找基准值并交换
// int baseIndex = new Random().nextInt(right-left+1)+left;
// swap(arr,baseIndex,left);
int baseValue = arr[left];
int i = left,j = right;
while(i!=j){
//从右往左找一个小于基准值的
while(i<j&&arr[j]>=baseValue){
j--;
}
//从左往右找
while(i<j&&arr[i]<=baseValue){
i++;
}
swap(arr,i,j);
}
//更新基准值位置
swap(arr,left,i);
if(i == k){
return Arrays.copyOf(arr,k);
}else if(i<k){
return quickSort(arr,i+1,right,k);
}else{
return quickSort(arr,left,i-1,k);
}
}
public void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 7.(medium)把数组排成最小的数
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
示例 1:
输入: [10,2] 输出: "102" 示例 2:
输入: [3,30,34,5,9] 输出: "3033459"
提示:0 < nums.length <= 100 说明:输出结果可能非常大,所以你需要返回一个字符串而不是整数,拼接起来的数字可能会有前导 0,最后结果不需要去掉前导 0
思路:
此题求拼接起来的最小数字,本质上是一个排序问题。设数组 nums 中任意两数字的字符串为 x 和 y ,则规定 排序判断规则 为:
若拼接字符串 x + y > y + x ,则 x “大于” y ; 反之,若 x + y < y + x ,则 x “小于” y ; x “小于” y 代表:排序完成后,数组中 x 应在 y 左边;“大于” 则反之。
根据以上规则,套用任何排序方法对nums 执行排序即可。
快排代码:
class Solution {
public String minNumber(int[] nums) {
//x+y>y+x x>y
//x+y<y+x y>x
String[] strs = new String[nums.length];
for(int i=0;i<nums.length;i++){
strs[i] = String.valueOf(nums[i]);
}
quickSort(strs,0,nums.length-1);
StringBuilder res = new StringBuilder();
for(String str : strs){
res.append(str);
}
return res.toString();
}
public void quickSort(String[] strs,int left,int right){
if(left >= right){
return;
}
String baseValue = strs[left];
int i = left,j = right;
while(i<j){
//找y大的 即y+x>x+y
while(i<j&&(strs[j]+baseValue).compareTo(baseValue+strs[j])>=0){
j--;
}
//找x大的 即y+x<x+y
while(i<j&&(strs[i]+baseValue).compareTo(baseValue+strs[i])<=0){
i++;
}
swap(strs,i,j);
}
swap(strs,left,i);
quickSort(strs,left,i-1);
quickSort(strs,i+1,right);
}
public void swap(String[] strs,int i,int j){
String temp = strs[i];
strs[i] = strs[j];
strs[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44